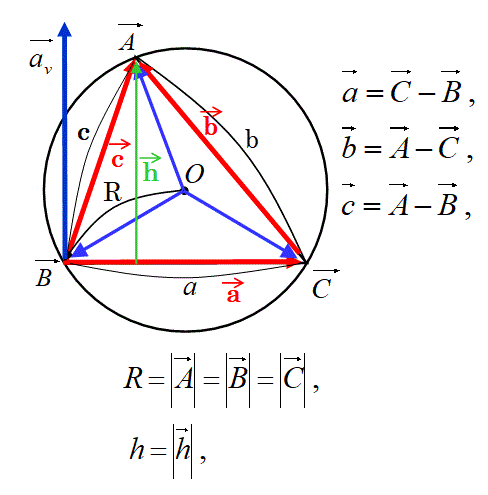
外接 円 の 半径 公式。 外接円の半径と三角形の面積の関係(S=4R/abc)
外接円とは?半径の公式や求め方、性質、書き方

ただし、いつだって正弦定理がすぐに使えるわけではありませんよね。 まとめ 中学流の外接円、いかがでしたか? 正弦定理のほうが確かに利便性は高いですが、 こちらの求め方も十分に使える手段だと思います! これからも、より良い外接円ライフを歩んでいってください! それでは!. ケージーの定理とその証明• 相似な図形の辺の比はそれぞれ等しいため、 ADについて解くと、 ADは直径だからその半分が半径。 なお、質問者様の立てた七次方程式をそのまま解いてみてはいませんが、質問に書かれた 考え方で立てた式であるなら、おそらく下のように、辺がクロスする図形も、条件を満たす 解として出てくるはずです。
宜しくお願いします。 よって、五角形を三角形と四角形に分けた際、 その四角形が「外接円を持たない円」であれば、 その五角形に外接円はできません。
平方根の長さを作図する2通りの方法• 共円多角形 [ ] 共円奇数角形の全ての角の角度が等しくなるための必要十分条件は、それが正多角形となることである。
三角形の五心と頂点までの距離• 必ず1つだけです。
2008 , , 128 1 : 17—48, :, ,. 三角形の成立条件とその証明• 8です。
五角形の外接円半径を求めたいのですが、、、

近似値ならいくらでも計算できますが。
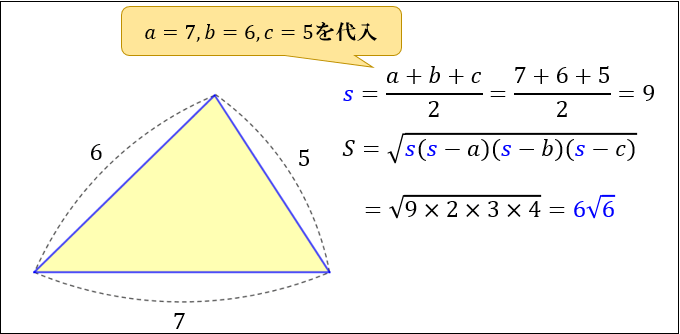
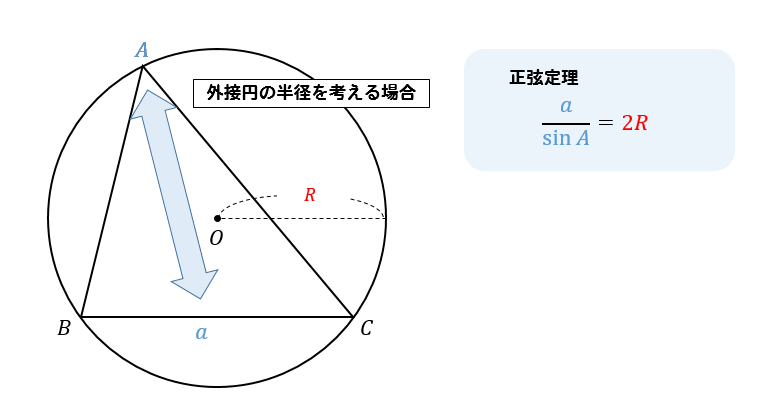
のとき、円 の半径を求めよ。 例題 一つ例題を載せておきます。
外接円の半径の求め方がイラストで誰でも即わかる!練習問題付き|高校生向け受験応援メディア「受験のミカタ」
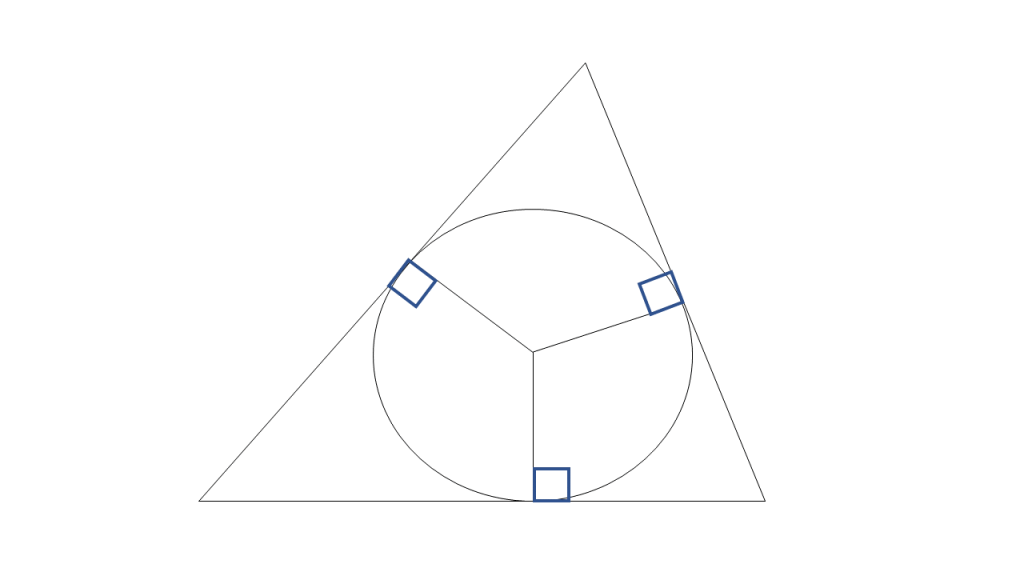
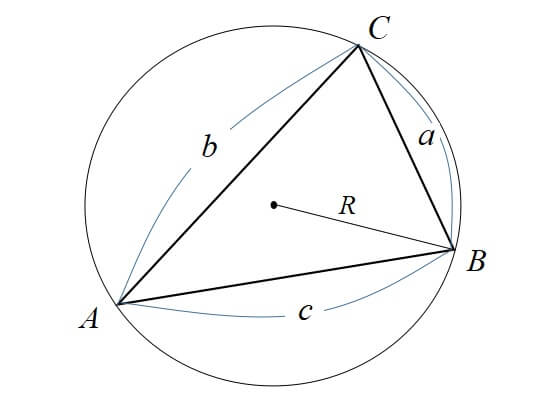
外接円を持つ多角形は、円 内接多角形 inscribed polygon , cyclic polygon 輪状多角形 あるいは、そのすべての頂点が同一円周上にある(つまり、である)ことにより 共円多角形 concyclic polygon などと呼ばれる。 トレミーの定理とその3通りの証明,応用例• 外接円のを 外心 circumcenter と言い、その半径を 外接半径 circumradius と言う。 外接円の式 [ ] における外接円の式はを用いて以下のように表すことができる。
三角形の1辺の長さとその対角がわかっていたら? まずは 1辺と対角のセットがないか探します。 ) この五角形を、一つの対角線で三角形と四角形に分割します。
この図形の外接円の半径、求め方教えてください!答えは4です!

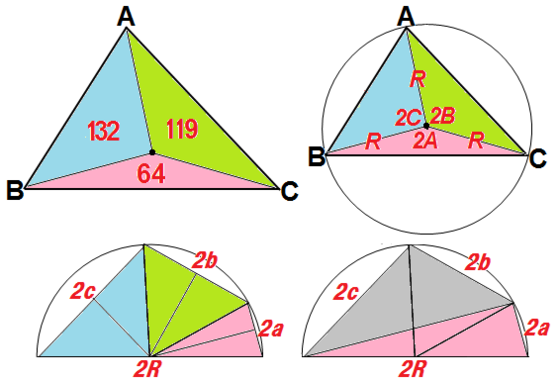
具体的に、どの公式をどういう場面で用いればよいか見ていきましょう。
11
三角形のの半径は、外接円の半径の半分である。
また、AからBCに垂線をひき、BCとの交点をHとします。
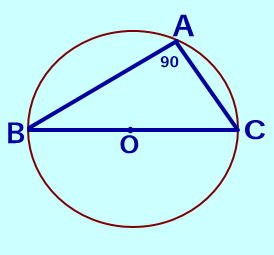
三角形が1つの円にすっぽりはまっている図をイメージするとよいでしょう。
の定理 また、 と 同じ弧の 円周角なので、 円周角の定理 すると、2つの直角三角形 は、 二組の角がそれぞれ等しいため 相似であることが分かります。
内接円 å¤


平面幾何の美しい定理4つ• はじめまして。
11
"Equiangular cyclic and equilateral circumscribed polygons," 95, March 2011, 102-107. 三平方の定理の4通りの美しい証明• まとめると以下になります。
ブレートシュナイダーの公式• 調和点列の様々な定義と具体例• To debug this try: debugmode true ; 式を見れば分かるように七次方程式が出現してくるのですが、多項式の解の存在についてなにも知らないため、これ以上手が出ない状態となってしまいました。
では、四角形などの外接円の半径はどのように求めればよいのか? こういうときは、四角形の対角線を引いて2つの三角形をつくり、 四角形の外接円はこれら2つの三角形の外接円でもあることに着目します。
接弦定理とその逆の証明など• よく似た概念の一つに () minimum bounding circle があり、これはその多角形を完全に含む最小の円を言う。
内接円 å¤

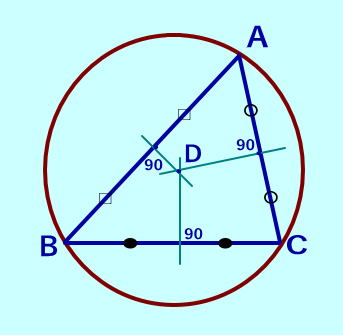
三角形の内接円とは 三角形の内接円とは、その 三角形の3つの辺すべてに接する円のことです。 シュタイナーレームスの定理• 三角形の五心の覚えておくべき性質を整理• 直観としては、五角形を、一つの対角線を共有させて三角形と四角形に分割するという操作で、絶対的に外接円を持つ五角形が作れるのではないかと思っているのですが、それすらも自信が持てなくなってきました。 こんなときは余弦定理を用います。
正方形の頂点と最短距離• 1つの三角形について外接円がいくつもあるといったことはありません。 また、最初に円を書いてその円周上に適当に5点をとって直線で結べば、 「外接円のある五角形」となります。
内接円、外接円の半径
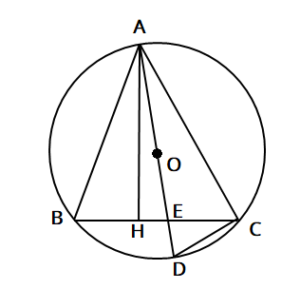
この直線が外接円とB側で交わる点をDとします。
6
複比の定義と複比が不変であることの証明• なぜ旨く行かないのか、教えていたただけないでしょうか? 数学の専門家ではないのでずれた回答になるかもしれませんが…。
だから、ある三角形の外接円の半径も、長さは1通りに決まるといえます。
円の方程式と関連問題|座標・ベクトル・複素数• これは内接円ですよ! 混乱に陥らないよう、ここで図のイメージをしっかり頭に叩き込むこと。
3辺の長さがわかっていて、角の大きさがわかっていないときは、まずは余弦定理を使って角の大きさを求めることを頭にいれておきましょう! 4:外接円の半径を求める練習問題 最後に、外接円の半径を求める練習問題を1つ用意しました。
【3分で分かる!】三角形の外接円の半径の長さの求め方をわかりやすく

射影平面の3通りの定義• allroots: expected a polynomial; found errexp1 -- an error. 何かの極限という形などでなく、具体的な解の値が必ず求められることが保証されているのは 4次方程式までです。 ヘロンの公式の証明と使用例• 三角形のフェルマー点の3通りの証明• ミケルの定理とミケル円• 円に外接する四角形の重要な2つの性質• すぐに正弦定理が使えないとしても、 余弦定理を組み合わせることにより、• ありがとうございます。 全ての三角形が二等辺三角形であることの証明!?• 平面,空間上の2点間の距離について• 根軸の性質と根心の存在定理• このような方法であれば、半径を求めるついでに各辺に対する中心角も計算できますので、 図を描くには都合がいいのではないかと思います。
6
三角形の中心(36個)を図示してみた• 注 [ ] 注釈 [ ] Trilinear Coordinates and Other Methods of Modern Analytical Geometry of Two Dimensions, Forgotten Books, 2012 orig. (式1) S=(abc)/(4R) 【解答1】 (解答おわり) この問題は、上の式のように、正弦定理を使って計算できます。 また, A M AM A M の中点が P P P , A N AN A N の中点が Q Q Q となるように M , N M,N M , N を取る。













