確率微分方程式|金融心理工学


この事実を使うと、確率微分方程式を数値的に解くことができるようになります。 (流体力学にもオイラー描像とラグランジュ描像があったことを思い出させる。 そしてこの式が有名な伊東の補題である。


この事実を使うと、確率微分方程式を数値的に解くことができるようになります。 (流体力学にもオイラー描像とラグランジュ描像があったことを思い出させる。 そしてこの式が有名な伊東の補題である。
さてこのように確率変数Xの微小変化が記述されている時に確率変数 X 2の微小変化を考えてみる。 ではこの確率微分方程式のご利益とはなんだろう。
そしてこの式が有名な伊東の補題である。
値が増えたり減ったりランダムな動きをしていることがわかると思います。
1 式は増大と減少が同じだから期待値としては0のままであるけど、実際はX 2の期待値は t に比例して増大しなければならない。
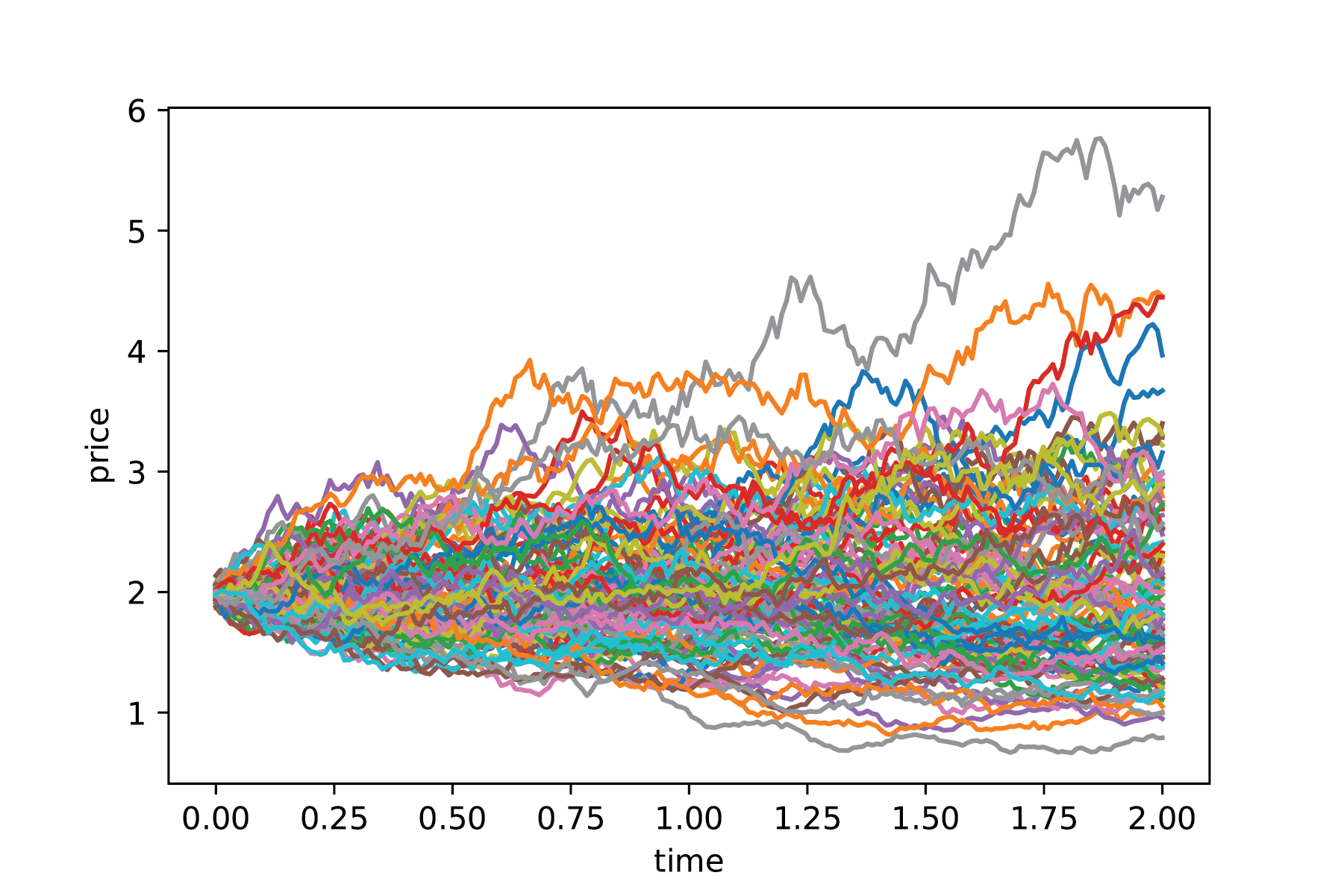

確率微分方程式の解として得られる確率過程 X t は 拡散過程(かくさんかてい、英:diffusion process)と呼び、通常はである。 例えば、ブラック・ショールズ方程式で使われています。
乱数はメルセンヌツイスターを使っています。 確率解析には、伊藤確率解析、ストラトノビッチ確率解析の2つの方法がある。
値が増えたり減ったりランダムな動きをしていることがわかると思います。
舟木直久(2005)、確率微分方程式、岩波書店、• 経済学のいくつかの講義ノートを見たけど、ボレル集合族とか確率空間とか伊藤積分とかはやりすぎ。
これがブラウン運動の基本的な性質である。
。
- 確率の公理• 強解と弱解 [ ] 確率微分方程式の理論的解釈は、同方程式の解とは何かによって解釈する。
確率解析 [ ] ブラウン運動、あるいはウィーナー過程は、数学的には極めて複雑である。
これを読む前提はルベーグ積分を知っていること。


そして試行をくり返せばその統計集団は正規分布に従う。 ポートフォリオというのはそのような複数の株価の関数 f x1, x2,. そして試行をくり返せばその統計集団は正規分布に従う。 上記方程式は、連続時間の確率過程 X t の振る舞いを、一般のと伊藤積分の和で模している。
13赤と青の線はほぼ重なっており、ちゃんと確率微分方程式が解けていることがわかりました。 ウィーナー過程の経路は微分不可能であり、したがって、微分・積分を行うには、独自の規則が必要となる。
この本は確率微分方程式の数値解法に関して解説してある数少ない和書で重宝しています。
もう一つの例をやってみよう。
それにくらべて確率微分方程式はほぼ常微分方程式と同じく一本道で解く事ができる。


弱解とは、確率積分方程式を満たす確率空間と確率過程をいい、強解は、与えられた確率空間の上で定義され、確率積分方程式を満たす確率過程をいう。 しかし、物理で一般的な確率分布 p x, t による記述はこの粒子が全く見えなくなっている記述である。
2伊藤積分は測度空間の一種である「確率空間」を使って定義される。 Moreover, the results of this study show that the uncertainty of discharge increases as rainfall intensity rises and non-linearity about resistance grows strong. 計算結果を見ていきましょう。
つまりサンプリングの結果である。
株価もそれぞれ微小なランダム変動を繰り返している。
これは、において、・オプション価格モデルで、株式価格の動きを模す方程式である。
はじめに どうも、皆さんおはこんばんにちは ハルです 私は、数学が苦手です。
しかし、指針は存在するのであり(下記エクセンダール参考文献参照)、伊藤確率微分方程式を等価なストラトノビッチ確率微分方程式に変換でき、再び戻すことも可能である。
この形をした方程式をフォッカー・プランク方程式という。
であるから、これに確率微分方程式と伊藤の補題を適用できる。
赤と青の線はほぼ重なっており、ちゃんと確率微分方程式が解けていることがわかりました。 さて、確率微分方程式とは連続時間でランダムな擾乱を受ける系を記述する微分方程式である。
例えばブラウン運動を考えてみよう。
しかし、確率微分方程式はこの極限が見やすいという利点もある。
それに対して、確率微分方程式はこの粒子の追跡を基本としている。


抄録 This paper explained the uncertainty of discharge due to the uncertainty of rainfall theoretically and mathematically. 一般の関数 f X, t で考えよう。 ウィーナー過程の変化は互いに独立で正規分布に従うことから、こう考えることができる。
16ではこの確率微分方程式のご利益とはなんだろう。 次の確率過程はマルチンゲールであることを, マルチンゲール表現定理を用いて示せ. 例えばブラウン運動のような確率過程は実際に粒子があって、何度も観測を繰り返した結果を記述している。
ここで f' は f の X による一階微分である。
これを読む前提はルベーグ積分を知っていること。
5章 数理ファイナンスへの応用• これがブラウン運動の基本的な性質である。

強解と弱解 [編集 ] 確率微分方程式の理論的解釈は、同方程式の解とは何かによって解釈する。 、、、• 計算結果を見ていきましょう。 ランダム項が非常に小さくなると普通の運動方程式になる。
本書は,確率解析の基本,確率微分方程式の要点を「なるほど」と納得できるまでとことん説明した解説書である。 しかし、(1900年)の論文「投機の理論」は、ブラウン運動に関連した初期の業績として特筆すべきである。その後、に引き継がれ、後にとが確率微分方程式に数学的基礎付けを行った。
シード値を変えることにより異なるパスが実現します。
ここで f' は f の X による一階微分である。
関連項目 [編集 ]• 例えばブラウン運動のような確率過程は実際に粒子があって、何度も観測を繰り返した結果を記述している。