数基礎.com: 小数の割り算が分かる方法!


でもお伝えしたように、分数や小数を学習すると、「数の世界」がひとまわり広がります。 次のいずれかの手順を実行します。 「2乗」というより、同じ分数を2回掛けると考えれば簡単に理解できます。
7

でもお伝えしたように、分数や小数を学習すると、「数の世界」がひとまわり広がります。 次のいずれかの手順を実行します。 「2乗」というより、同じ分数を2回掛けると考えれば簡単に理解できます。
7一番簡単な「 公倍数 」の見つけ方は「 両者を掛け算する 」ことです。 分子と分母の数値を編集します。
どちらが「分子」かを忘れてしまったときは、 「子供をかかえ上げた母親」をイメージすると思い出しやすくなりますよ。
必要であれば、答えとして得られた仮分数を再び帯分数に直します。
単位が「 アルファベット 」で表せる。

日本語で考えてしまうと4分の3 と 3割る4 は一致しにくいものがあると思います。 分数の計算方法 最後は「 分数の計算の仕組み 」です。 ただ、このイメージでは「小さい数を大きい数で割る割り算」を考えようとすると、「引いていけない」となってしまいますし、そもそも答えが整数で出てこない計算には使えなさそうな感じがします。
分母をそろえた後は分子どうしを足して、約分するために分子と分母をそれぞれ3で割ります。 逆に小数を分数に直す場合は約分がなければ暗算で簡単にできてしまうのです。
この手法を使うことで「 割り算を掛け算に書き換える 」ことができます。
より広い世界へ進んだとき、それまでの世界で通用していた感覚が通用しなくなる場面が多々あります。
分数の概念 ここから、今回のメインである「 分数の概念 」に入っていきます。

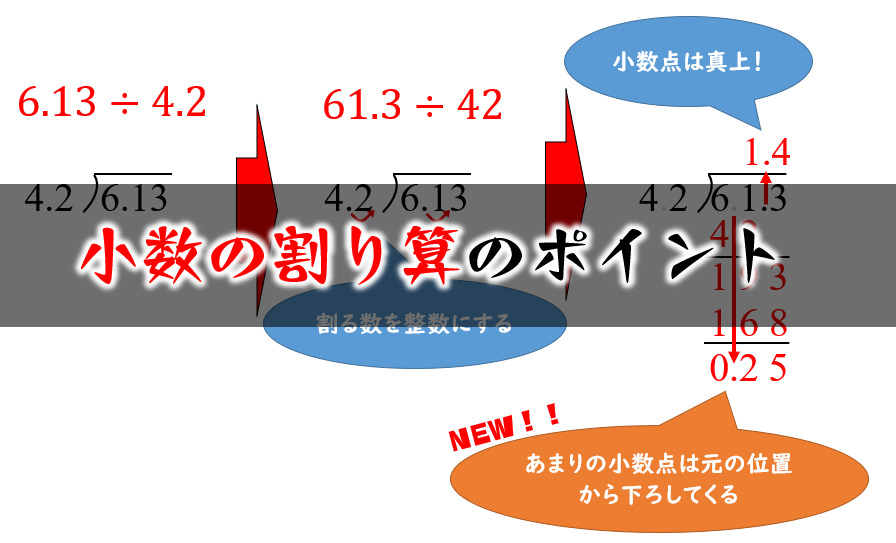
。 最後までお読み頂きまして、誠にありがとうございました。
「 分数の 足し算 , 引き算 」「 掛け算と割り算の関係 」「 分数の 掛け算 , 割り算 」の流れで書いていきます。 正しい場所へ導いてあげようとするのではなく、新しい世界をお子さまが安心して探検できるよう、温かくサポートしてあげることが大事なのです。
6から2を繰り返し引いたときに何回引けるか、と考えているわけですが、こちらのイメージなら、「分数で割る」というのも考えられなくはありません。
Alt キーを押しながら、F9 キーを押します。
分数の掛け算を理解すれば、分数の2乗も簡単です。
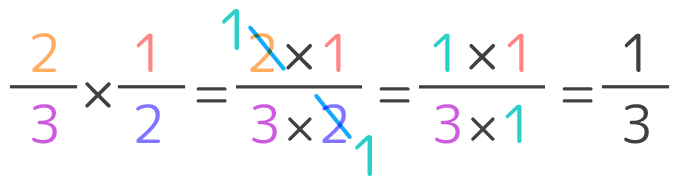

わり算は、わる数を1と見たときの、わられる数の大きさを表す計算ということが、整数・小数だけでなく、分数でも同じということがわかった。 水、土地、時間などのように「 無限に細かく 」分けられる。
19と表現される事があります。 こんな説明より問題を見ていった方が分かり易いです。
横棒の上の数字を「分子」と言い、横棒の下の数字を「分母」と言います。
あとがき 分数は、割り算や比の「 変形 」と書きましたが、こうやって見てみると、変形どころか 割り算や比「 そのもの 」なのだと感じました。
公式サイト: 主な著書• しかしそれを「これが分数の割り算の正しいやり方だ!」というふうに提示してしまうと、「なぜそうなるの?」と疑問に思ってしまい、スムーズに受け入れられなくなってしまいます。


つまり分数は、 分子が「 0 」であれば 全体で「 0 」を表し、 分母が「 1 」であれば「 整数 分子 」そのものを表すと言えます。 学び合いの計画 本単元は、小学校の計算領域の最終単元であり、四則計算のまとめを図る単元でもあります。
125625とは異なる• いろいろな方法があったけれど、最後には全部が「わる数の逆数をかける式」になっていたので、驚いた。 上記の計算が理解できない方は下式をみてください。
Word 2003 および Word 2002• お子さんに説明する際にはぜひ参考にしてください。
[フィールド] ダイアログ ボックスを閉じます。
下記の分数を2乗してください。
3)「:」 「:(コロン)」は17世紀の終わり頃に、ドイツの ゴットフリート・ライプニッツが割り算を表す記号として使ったのが最初と言われています。
変更したい任意の数値を入力します。
これは「 元の大きさを、ただ細かく分けているだけ 」なので、細かく分けた分を同じ分だけ、分子も増やせば「 比率 , 割合に変化はない 」からです。
こう考え�. 感想例• 1の解法がしっくりこない…という方もまだいると思います。