いろいろな確率分布の平均,分散,特性関数などまとめ
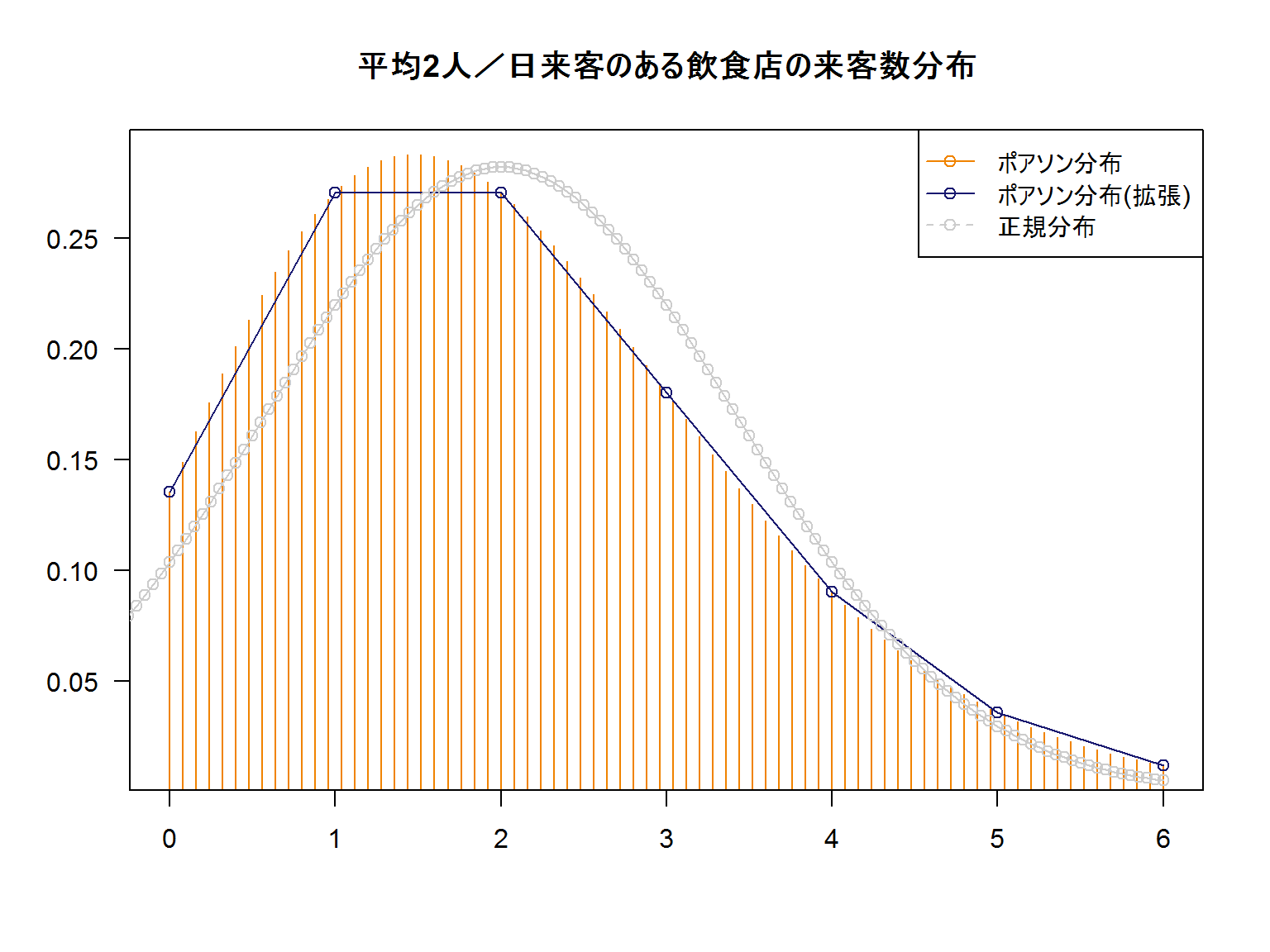

1ミリリットルの希釈された水試料中に含まれる特定のの数 (細菌数検査における)。
6この記事の最初の方に「ポアソン分布は 単位〇〇あたりの回数」と書きました。
下は17個,上は38個発生させました。
設問[1]〜[2]があり、以下それぞれについて確認します。
上記より、 は下記のようになります。
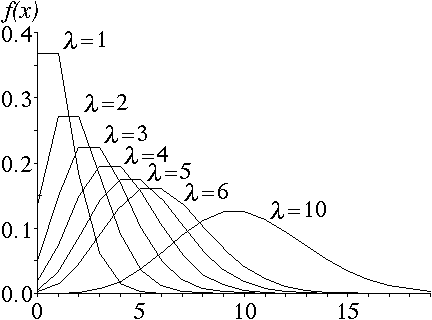

しかしこれを文字通りに受け取ると,1単位時間に 0 回事象が起きたとき,誤差は 0 であると誤解してしまいがちです。 次期バージョンでは直ります。 ポアソン分布の導出は二項分布からネイピア数を用いて導出する方法や、微分方程式を用いた方法などがある。
10ここで の平均は に 、 、 を代入して、 となる。
一般にポアソン分布の差(Skellam分布といいます。
[1] ・Answer 平均も分散も で求められるが、以下でその導出を行う。
和をとって正規化する必要があります。


1人しか患者さんが運ばれてこない確率• 多くの場合、分布がどのように発生するかについての単純な確率モデルを用意すると便利です。 Double Poisson分布 正規化項を別途計算しないといけないので少し複雑になっています。
単位日数あたりが分かったということは、例えば「2か月で猫に会う回数」を計算することができるようになります。 詳細は、これまた前回の記事「」をご参考ください。
エクセルでは下記のようにあらわします。
2番目の下波括弧の部分には n が出現しないので、そのままである。
感覚的には納得いきませんが、このように数学的に定義されていますので、単純に「ゼロの階乗は1」と覚えましょう。

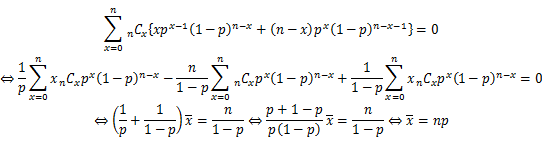
今回の問題は猫に会う回数が増えたか?という質問で 方向性があります。 関数形は以下です( 、 )。 Ladislaus von Bortkiewicz 1898 PDF , , University of Wasington Library, Leipzig Druck und Verlag von B. 上記の は であり、一定です。
ポアソン分布の導出(微分方程式ver) にまさにそれが書かれていました。
同じ事象を逆の視点で見ていることになります。
は k のを表す。
ポアソン分布の分散はカウント数に等しいのでそれぞれ100と149で,差の分散は分散の和ですので249です。


test 10 と打ち込んでみましょう。 1962 A queuing model with state dependent service rates. また、仮定1から互いに背反する期間では現象が起こる確率は独立のため、同時確率は各々の積で表される。 個別の事象の発生は珍しいけれど、無視はできない事象についての確率分布です。
9overdispersion(過分散)な分布は個体差&分布で説明するのがシンプルで解釈しやすくて、個人的には好みです。 一般化分布(generalized Poisson distribution, Lagrangian Poisson distribution) のページは見つかりませんでした。
[2] Consul, P. なお、どの分布も1chainあたり1秒以内に収束しました。
参考文献 [1] [2] [3] [4] [5]. 1時間という長さでは2人以上来るでしょうが、1分間、1秒間という微小時間でとらえれば、その間に2人以上来ることはないと仮定します。
次に、その例を示す。
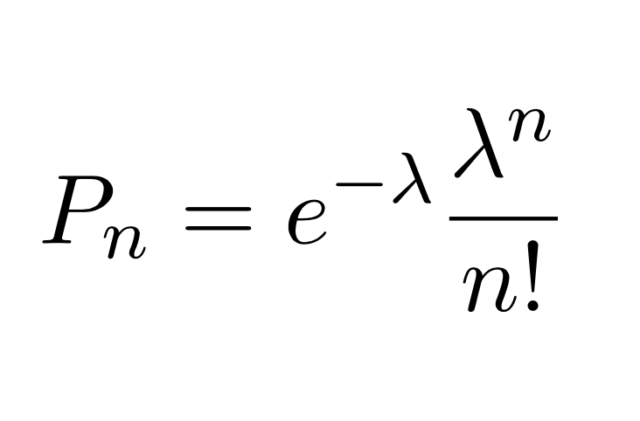

分布の導出と簡単な解釈について確認できたので1節はここまでとします。 この後の論文([11])を読むと分かりますが、同じ種類の植物でも調査の場所によって分布がかなり異なるようです。 Conway--Poisson分布 上の式のままだと の値が大きくなりすぎてが非効率になります。
Technometrics, 15, 791-799• Teubner , 復刻版がにより発売されている• Par Simeon Denis Poisson 1857 PDF , , Des Regles Generares du Calcul des Probabilites, Bacheliar, Impremeur-Libraire. [5] 関数形は以下です( 、 )。
を求めると、以下の確率分布表のようになりますね。
最初の等式での合計の開始点を番目のインデックスに "スキップ"しますこれは、任意の、、、正確に製品の1つの項はゼロです。
が と比べて小さくて、 が大きい時にPoisson分布になります。