いろいろな角度を求める問題1 図形の等辺を利用する


*問題は追加する予定です。 今回は、 三角形の角度を求める問題を解いていきたいと思います。 この問題では、 錯角の性質を使います。


*問題は追加する予定です。 今回は、 三角形の角度を求める問題を解いていきたいと思います。 この問題では、 錯角の性質を使います。
また地平線は水平な直線とします。 でもこれは、どうしようもないです。
でしたら、なぜ分度器を使う授業があるのかというと、「角度の感覚をつかむ」ためだと思います。
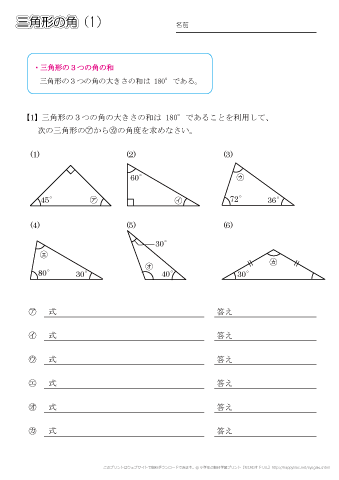
練習問題をダウンロード 画像をクリックするとPDFファイルをダウンロード出来ます。
ただし,星A,B,Cは 北極星の周りを24時間かけて反時計回りに1周します。


普通に生活していく上で、「角度」を気にする必要はありませんから。 辺の長さが等しいわけですから、4つの辺に、長さが等しいという印をつけておきましょう。 ---------------------------------------------------- 午後6時30分, 北の空に北極星Nと直角二等辺三角形の形になる星A,B,Cが 図のように見えました (Nの左にB,Bの上にC,Cの左にAで,NB=BC=CA)。
4Copyright C 2019 Alpha. ご自由にリンクしてください。 3. 下の図のそれぞれの角度を求めなさい。
1 2 3 5. 下の図のそれぞれの角度を求めなさい。
当サイトの文章・画像のリンク以外による無断使用、転載はお断りいたしております-• AH=4cmなので、 GH=4cm。
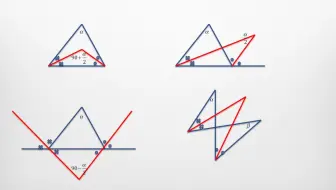
最初の2枚は説明になりますが、角度にとって重要なものなので必ず覚えてもらいたいところです。

まぁ要するに、そんな感じのことになってくる「角度」が始まります。 分度器で角度を図るのは、「角度」の単元では最初の方だけだと思います。
広告ブロックをオンにしたブラウザーではページを表示できません。 道具の1つとして挙げたのはそんな理由からです。
1 対角線が77本引ける多角形は何角形ですか。
平行じゃない場合も同位角と言いますが、図形問題では全く使いません!あくまで平行であることが条件です。
理解していないと、勉強を進めていけないほどには。

今はまだ大丈夫でしょうけど、この先苦しめられることになる「角度」です。 はじめはなかなか思い浮かばなくても、様々な問題を解いていくうちにコツがつかめてくるので大丈夫です。
19「このくらいだと何度」という感覚をつかもう 「角度」です。 その他のコンテンツ• 補足:円周角は道具じゃない? 受験サイトや受験ブログでちょっと話題になった入試問題があります。
もちろん、その前提として、たとえば、「二等辺三角形は2つの辺の長さが等しい」だけではなく、「二等辺三角形は二等辺に向き合う2つの角も等しい」ということが反射的に出て来なければなりません。
そのあと星Cが沈みました。
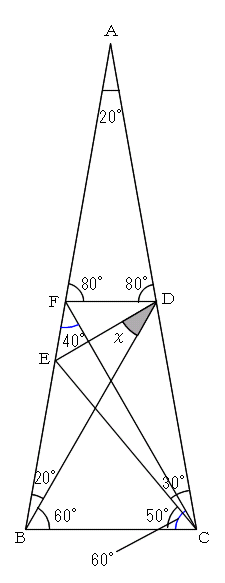
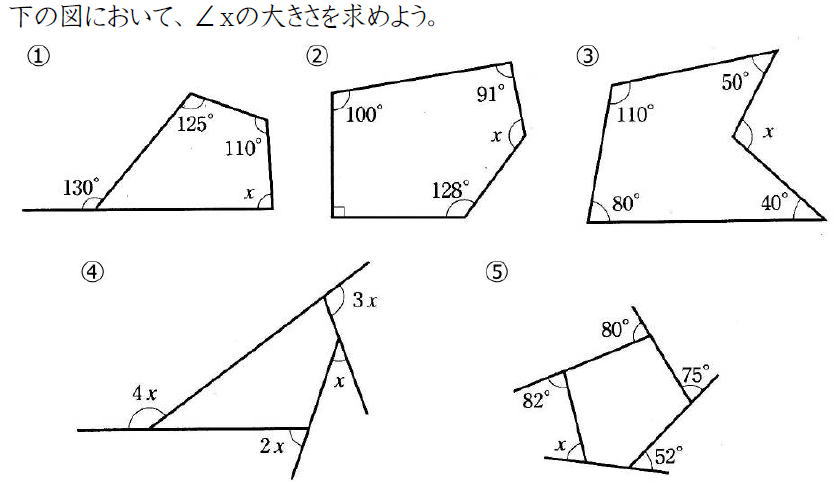
工夫していろいろな角度を求める問題です。
1 2 3 4 四角形ABCDは平行四辺形 AとBは平行 5 ア=イ 2. 次の各問いに答えなさい。
このページはリンクフリーです。
その場合は、 自分の求めたい角度と等しい角度はないかを探しましょう。
そこで、補助線をひいて、三角形を2つにしてしまいましょう。
1. 下の図のそれぞれの角度を求めなさい。

2本の平行な直線において同位角は等しい というものです。 過去入試問題より・・・よく出る角度の基本問題 今回も特定の中学校の入試問題というわけではなく、入試にもよく出題される角度の基本問題で鍛えておきましょう! と言うか、二等辺三角形・正三角形の問題なのですがね…。
8五角形以上の多角形の内角の和は決まっていて、三角形や四角形に分割すれば、すぐに割り出せること。
「角度」というものを子どもたちに認識してもらうには、分度器を使って実際に角度を測ってみるというのは、それなりに有効でしょうから。
なので、算数の問題で「分度器で角度を測ろう」というものは、さほど重要視されていないと思います。
右図のようにして、補助線をひきます。
1. 下の図のそれぞれの角度を求めなさい。 わかりやすく赤で書きました)を引くことで解きやすくなります。
三角形の内角の和は180度であること、四角形の内角の和は360度であること。
三角形AGHは正三角形。
1 2 3 四角形ABCDは正方形 五角形EFBGHは正五角形 五角形EFBGHは正五角形 八角形ABCDEFGHは正八角形 6. 下の図のそれぞれの角度を求めなさい。

等しい長さの辺を探して二等辺三角形を探すようにして問題を解いてみましょう。 もっと根元に言及しておきますと、 「こんなのおかしいや!」「こうだったら分かるのにな!」という思いが乏しいか、これを燃焼させて解決する術を見出せないという点が合格者との決定的な差になっています。 もチェック!! もチェック!!. 実生活で「角度」を気にしながら生活してしている人は、ごくわずかだと思います。
5問題PDFは全4ページ分。
当サイトのコンテンツは、個人使用に限り無料となります。
1 2 AとBは平行 AとBは平行 7. 下の図のそれぞれの角度を求めなさい。
要するに、問題と自分の基本知識を結びつける回路が、訓練によってできていない、しかも教訓として刻み込まれていないということが元凶にあります。