長方形の面積を求める公式の数学的な意味 | Note&Board


6 を代入すれば、面積は16cm 2となります。 1 高さが等しい三角形と面積比(等高三角形の面積比、区切り面積) 2 台形・平行四辺形・長方形と区切り面積 3 三角形の辺の比と面積比(隣辺比) 4 影の問題(三角形の相似の利用) 学習項目は4つで少なく感じられるかも知れませんが、 それぞれの学習内容は非常に濃いものです。 つまり, 面積は図形から数への対応,図形から数の関数と見ることができます。
17

6 を代入すれば、面積は16cm 2となります。 1 高さが等しい三角形と面積比(等高三角形の面積比、区切り面積) 2 台形・平行四辺形・長方形と区切り面積 3 三角形の辺の比と面積比(隣辺比) 4 影の問題(三角形の相似の利用) 学習項目は4つで少なく感じられるかも知れませんが、 それぞれの学習内容は非常に濃いものです。 つまり, 面積は図形から数への対応,図形から数の関数と見ることができます。
17このm(F)が面積です。
など,一つの要素「国」が,必ず一つの要素「首都」に対応する関係をいいます。
正方形の方が面積が大きいです。
要するに,「(2)満たすべき法則」の意味は, ・ 合同のときには,同じ数を対応させる ・ 図形の和,重なりのない和ならば,それに対応する数も和とする この2つを満足するように,図形に数を対応させたものが面積です。

ところが,無理数の場合は,共通する単位が存在しないので,有理数のように整数に直して考えることができません。 問題はランダムで変わるため、面積問題に慣れるためには役立つと思うのでぜひご活用ください。
15サクサク計算できる、 必殺のコツを身につけたと言えます! … <おまけ> こんな質問を、よくいただきます。 サピックス小5の第34回で学習する 「等高三角形の面積比(あるいは区切り面積)」 「隣辺比」 「相似の利用」 はその中でもよく出題される分野のひとつですから、 受講前の準備(既習範囲の知識の確認)、 受講後の復習(解法の習得と使い分け方)に取り組んで、 「辺の比と面積比の問題はバッチリ!」 といえるようになれるといいですね。
「分数」を使うと「何を求めているのか、わからなくなる」という場合は、 このように整数だけで計算できる方法を試してみてください。
半径がわかれば、すぐに面積もわかります。
これと同様のことを直方体についても考えればいいのです。
【工夫した解き方. 正方形なら容易に敷き詰められます。 これより,• 1 ~ 3 でつまずく可能性がありそうでしたら、 三角形の底辺と高さの関係を授業までに確認しておきましょう。 単位とする図形の 適切な図形 ・ 正方形ならば,縦と横の長さが同じであることから,それらを別々に考える必要はなく縦と横の数値を同じように測定・計算できる。
「圧力の分野で、面積の計算が…。 その理由は,隙間なく埋め尽くせることが必要だからです。
。
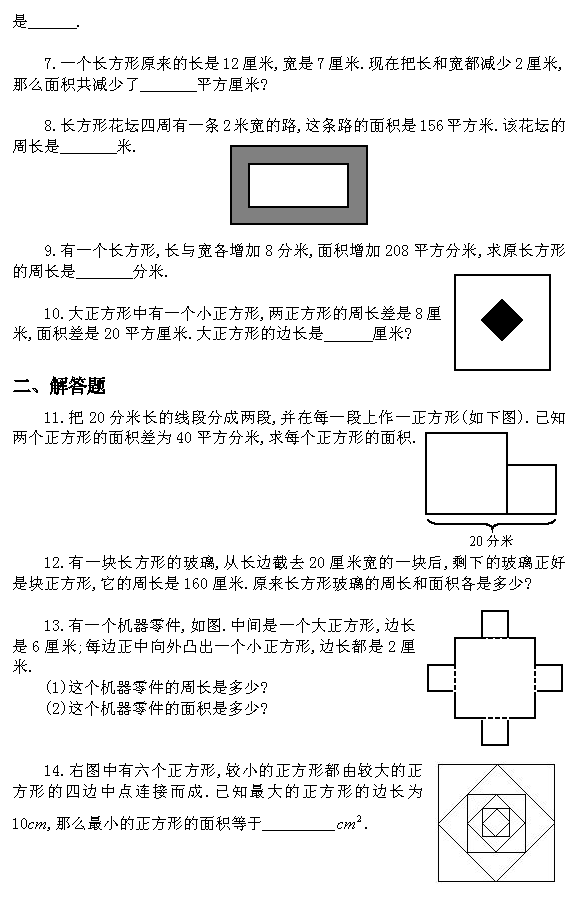
【問題1】 さてそれでは、任意の長方形から同じ面積の正方形に作図する方法を考えてみて下さい。
すると、中心角の角度も114. 台形の3辺と高さから、残りの1辺と面積を求めます。

5m 最難関中では 「立体図形の影問題」 「光源が移動する影問題」 「移動する人の影の長さとグラフの問題」 のように、 今回の学習事項にもうひとつの要素を 追加(例:立体図形であれば2つの投影図を利用する)して解く問題が出題されます。 扇形はどうでしょうか?下の図のような半径が4cmの扇型を考えてみましょう。
11では、次に長方形を考えてみましょう。
そこで,数の拡張を考えます。
つまり,周の長さが一定である長方形の中で,面積が最大のものは正方形。
関数とは,例えば,「アメリカ合衆国」の首都は,「ワシントン」です。

000001平方厘米 市制:• 3 は6年生でも苦手にしているお子さんが少なくない、 高度な学習な項目のひとつです。 ですから、「1m = 100cm」という 長さの法則が分かるだけで、 次の式が理解できます。
16では、二等辺三角形はどうでしょうか? 底辺が6cmの二等辺三角形の面積を考えてみましょう。
仮にAB=5cmとすると、次のような解き方になります。
中学校では、任意の四角形から同じ面積の三角形を作図するという、平行線を利用した「等積変形」というものを習います。
面積は横の長さの数値に比例することと実数の連続性から,辺の長さが無理数であってもかけ算で求められます。


【E問題-1 2 】 右図で、BPとCPの長さは等しく、AQとCOの長さの比は4:1、ARとBRの長さの比は1:3です。
双曲線の弓形の面積と弧の長さを計算します。
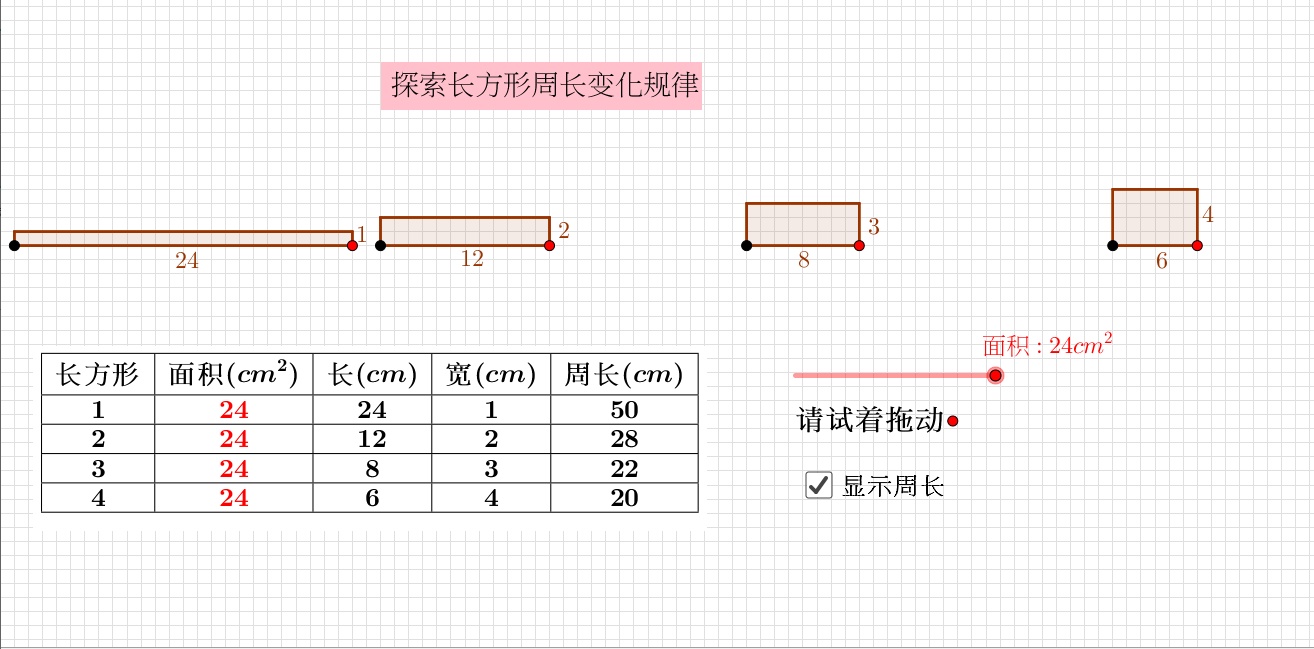
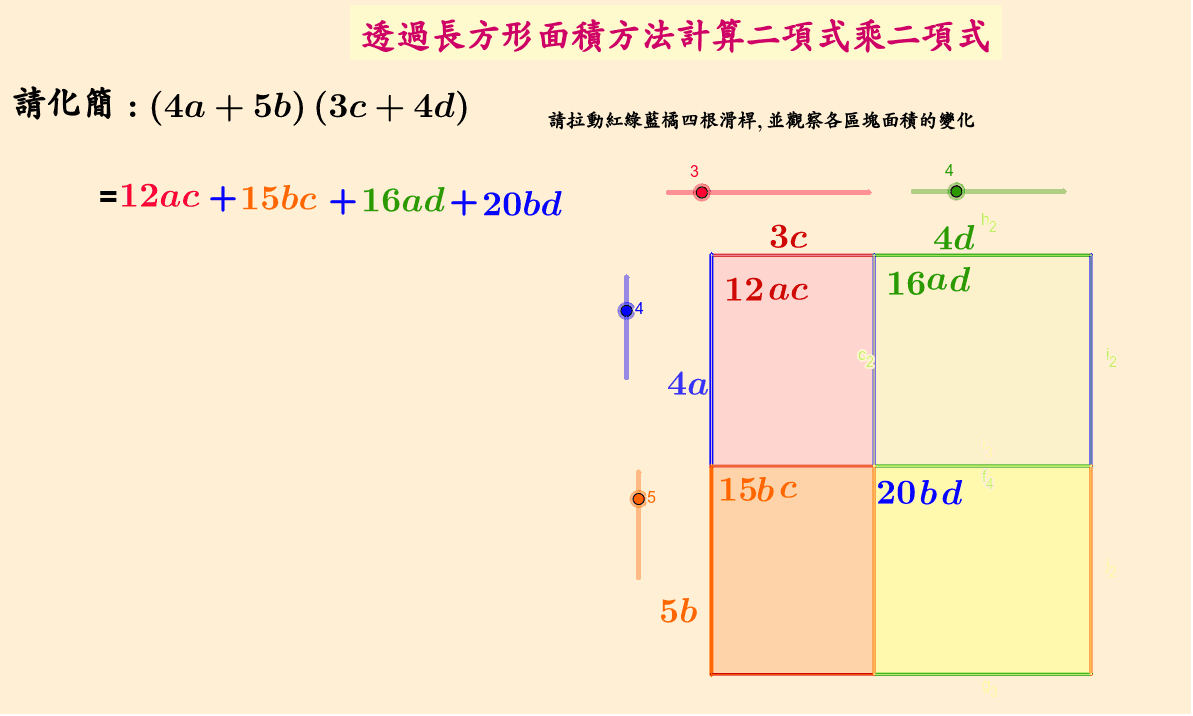
1㎠の正方形が縦に3つあり、横には6つですから これは「足し算」ではなく 縦3つの正方形が横に6つあると考えることが出来るので 「かけ算」 で面積を求めることになりますよね! これが長方形の面積を求める公式の考え方です。
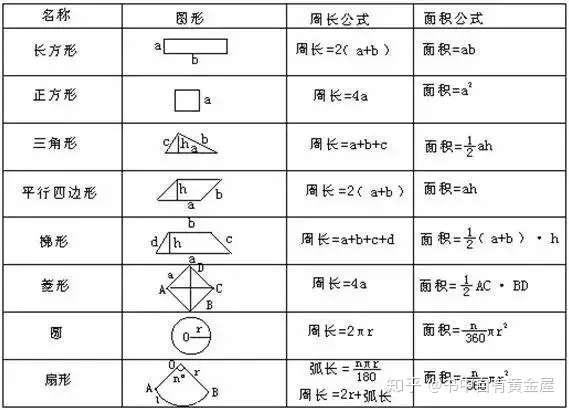
正n角形の辺の長さから面積,周囲の長さ,頂点の角度,対角線の本数を計算します。
2 面積の数学的な意味 (1)図形から数への関数 面積は広さを単位のいくつ分かで表した数であり,面積を求めることは対象の図形に敷き詰められる単位正方形の数を求めることである,と説明しました。
四角形の4辺と向かい合う1組の角の和から四角形の面積と周囲の長さを計算します。
だから,その単位分数を考えれば,長方形の面積は,かけ算で求めることができます。
数値はランダムで変わり無数に問題を作ることができるので、ぜひご活用ください。
「共通角をはさむ2辺の積=面積比」 を利用する解き方です。