円錐表面積求め方。【計算公式】円錐の表面積の求め方がわかる3つのステップ

【3分でわかる！】円錐の体積・表面積の求め方

母線と半径の長さが変わっても、弧の長さと円周の長さを等しくするために同じようにして中心角が決定されます。

もくじ• なぜなら、円錐の問題には空間図形の知識だけでなく、おうぎ形の知識も一緒に問うことができるからです。

いずれにしても、表面積の求め方の基本は表側の面をぜんぶ描くということです。
そのため四角錐では、四角形（底面）と三角形（側面）の面積を計算すればいいです。
同じ大きさの円が上下に２つと、中ほどに長方形が１つできます。

円錐の表面積、中心角を求める問題を丁寧に解説！

円錐の頂点から垂線を下ろし、その垂線を含む平面で断面図を作ると以下のようになります。数値はランダムで変わり無数に問題を作ることができるので、ぜひご活用ください。都道府県別の受験対策もバッチリ！• なぜかというと、底面積の2つの円の体積を求めるのは、体積と変わらず難しくありませんが、側面積の長方形の面積を求めるのが少々厄介だからです。

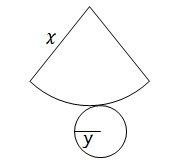
円錐の側面を展開すると、扇形になります。公式は以下になります。

必ず同じ数値になるわけではないので、間違った覚え方をしないように気をつけてください。
公式を使わなくても、もちろん答えは同じになりますので、ぜひ皆さんの手で計算してみてくださいね。
これらそれぞれの面積を求めます。

円錐の表面積の求め方

これらの性質を利用することで、中心角や扇形の面積を計算すしましょう。ですが、これを活用しない限りは現状は変わらないです。このとき、1つの四角すいの高さは、立方体の高さの半分になります。

ここで、図に赤線で示した「扇形の弧」と「底面の円周」は、もともと接していたため、長さが等しいことに注目します。そのため、以下のようになります。

母線を10㎝、半径を6cm、円周率を3. （1）底面が1辺6cmの正方形、側面はすべて合同で底辺が6cm、高さが5cmの三角形の四角錐。
さらに「扇形の弧の長さ」が「底面の円周」と等しいことに着目すると、以下のようになります。
角柱・円柱の応用問題にはなりますが、これまでの知識を利用することで、公式を使いながら答えを出せます。

円錐台の体積と表面積を計算する公式と証明

$方求め円錐表面積$ 方求め円錐表面積

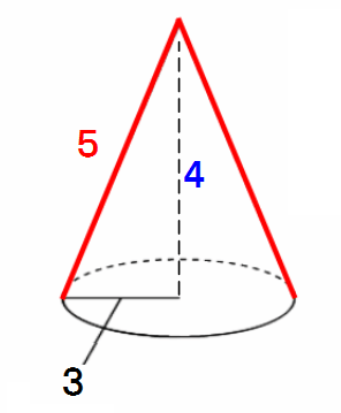
そして錐体には角錐と円錐の2種類があります。三平方の定理より、この円錐の高さ（下ろした垂線の長さ）は4になりますね。中心角の求め方をまとめておきましょう。

この方法のメリットは• これらを合わせると表面積を求めることができます。

今回は方程式を使って求める方法で紹介します。
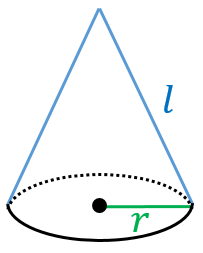
言葉で言うとわかりにくいので、図１を見てください。
図１の青色の線の部分が母線になります。

円錐の表面積の求め方

ということで、この記事で三角錐の体積と表面積の求め方をマスターしてしまいましょう！この記事では、最初に公式や基本事項を確認して、公式の証明を丁寧に解説し、最後に練習問題にトライします。円錐の側面積の求め方側面積は扇形なので、扇形の面積の公式を書き出しましょう。立方体でなくても直方体でもよいのですが、切り分けた四角すいの形が違うと一目で体積が等しいとはわかりにくいのであえて立方体を使って説明します。