【中3数学】多項式を因数分解して2次方程式の解を求めるやり方を解説!


そんな想いで無料の体験授業を実施しています。


そんな想いで無料の体験授業を実施しています。
以下の形を思い浮かべてください。
先程解説したポイントを当てはめると「足すと9に、掛けると18の数になる」数の組み合わせを考える必要があります。
因数分解の公式の見分け方 実際に出題される因数分解の問題では「この公式を使って解きなさい」のように、使用するべき公式を教えてくれません。
この計算を見て気づいた人もいると思いますが、 左辺の たし算の式が右辺で かけ算の式になっています。


では、(式1)を解いていってみましょう。 一方の例題2は、 文字に置き換えた後、 置き換えた文字を共通因数として取り出すパターンでした。 ちょっと具体例を見てみましょう。
18このように、よくわからない説明が書かれていると思います。
この「 共通因数でくくる」というところが大きなポイントです。
つまり、 「 因数分解」していることになりますね。
無料の体験授業で、 「たった15分の勉強で、今までの3倍の効果を出せる勉強方法」を無料体験で実感してみませんか? 勉強が苦手な子ほど、ほんの少しのキッカケで必ず変えてみせます!. (式2)の方はもうひと手間必要です。


中学校で勉強する因数分解の公式は以上の3つです。 ですので、「2xy」を「4xy」に合わせてあげればいいんです。 例題1は、 文字に置き換えた後、 公式を使って因数分解するパターンでした。
15ここまで来たら、後は例1と同じなので大丈夫ですね。 共通因数がない因数分解の例題 次の式を因数分解せよ。
因数分解の単元ではこの公式こそが大きな敵で、テストでも点数に差がつくポイントです。
これを共通因数でくくりだす因数分解といいます。
また 10aは、aと5をかけた 5aの2倍になっています。
ぱっと見た感じでは共通因数が見当たりません。 また上の例では、因数分解した結果、 x+3 と x+8 のかけ算になりました。
上図のように、多項式と因数分解をした式を決めたとき、これらが恒等式となるには、 という関係を満たす必要があります。
このパターンの因数分解について、例を挙げてみましょう。
3と6であれば足して9に、掛けると18になる組み合わせを満たすことができます。
withコロナ時代を乗り切ろう• この手順を守って因数分解の問題に取り組んでみてください。 下の図のように、 かけ算の式をたし算の式にすることが「 展開」、 たし算の式をかけ算の式にすることが「 因数分解」です。
以下の例題を一緒に考えてみましょう。
忘れないように気を付けましょう! 別パターンの、文字に置き換える因数分解の問題を見てみましょう。
1 x 2-36y 2 2 25x 2-9y 2 解答・解説は以下の通りになります。

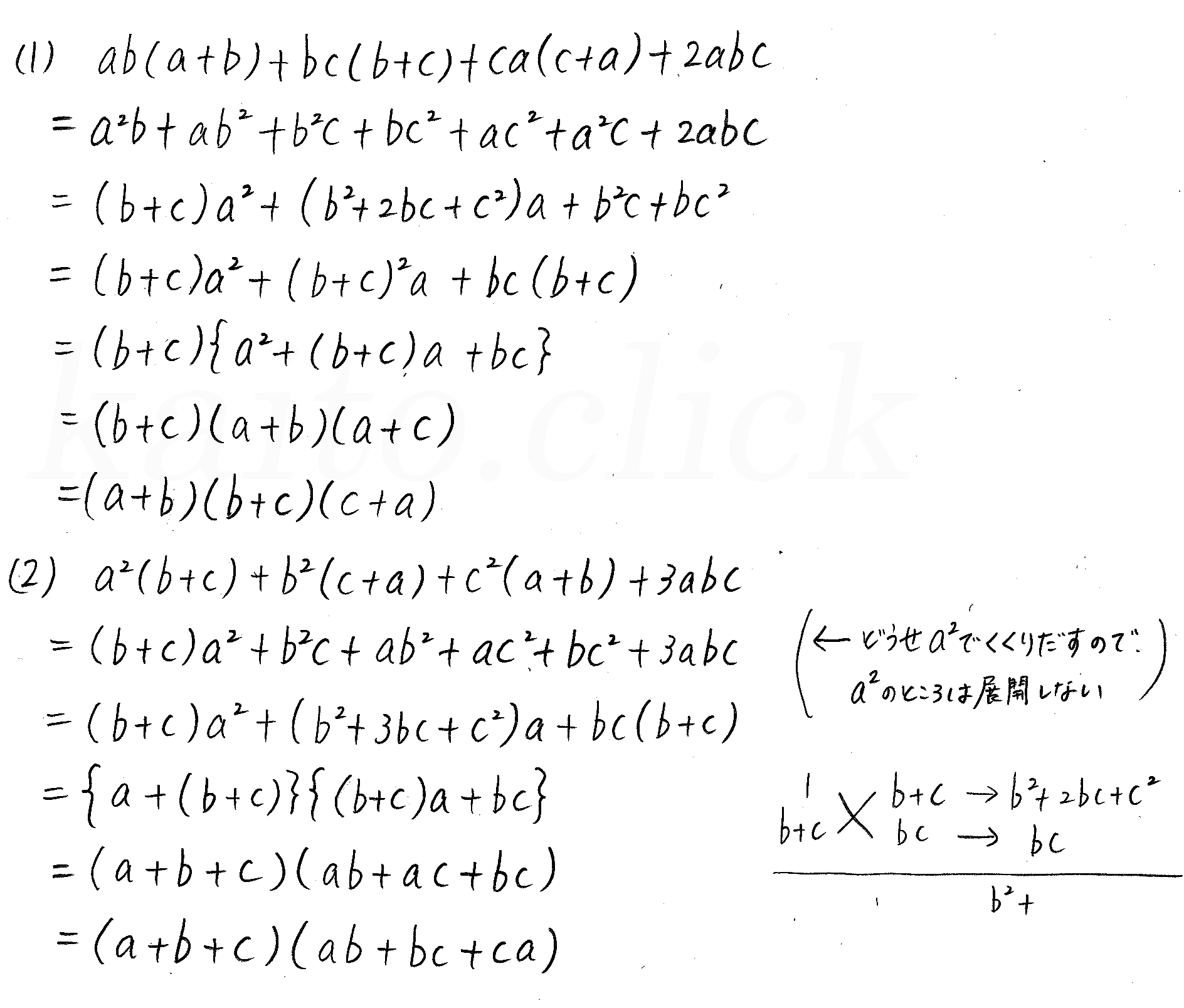
因数分解の基本 因数分解とは言葉で言えるものの、それを説明できる人は少ないのではないでしょうか。 ここからは実際の定期試験でどの公式を使えばよいのか判断する方法についてをお伝えします。 今までやってきた計算は【展開】です。
1小学生• それを踏まえた上で• まずは乗法公式を確認しておきましょう。 ジャニアスについて• 先に共通因数を見つける方法を紹介します。
共通因数がない問題もあるので、その解き方は次の章に書いておきます。
3が共通因数と分かったので、3で式をくくります。
・x 2+9x+20 まず、 かけ合わせて20になる数の組合せを考えてみましょう。

読み方は 「ルート」と読みます。 このパターンの因数分解について、例を挙げてみましょう。
無理な勧誘は一切無いことをお約束いたします。
練習問題を解こう(その2) 練習問題2 次の式を因数分解しなさい。
では、なぜ因数分解をする必要があるのか、どんなやり方で因数分解をするのかをみていきましょう。
Contents• そこをミスしないように気をつけてくださいね。