【C#】ナップザック問題を解いてみる
特定の解法が常に優れているのではなく、問題に応じて適切に解法を選択するのが重要であるといえそうです。 1 貪欲法について 近似解を得る方法としてまず最初に思いつくのが、「重さあたりの値段(以下コスパと呼びます)が大きい ものから順に入るだけナップザックに詰めていく」という愚直な方法で、「貪欲法」と呼ばれています。 見覚えがありますね。
11
特定の解法が常に優れているのではなく、問題に応じて適切に解法を選択するのが重要であるといえそうです。 1 貪欲法について 近似解を得る方法としてまず最初に思いつくのが、「重さあたりの値段(以下コスパと呼びます)が大きい ものから順に入るだけナップザックに詰めていく」という愚直な方法で、「貪欲法」と呼ばれています。 見覚えがありますね。
11今回はこの例でやってみます。
なお、2列目以降の表を埋めていく部分をプログラム(Python)で書くと、下のようになります。
動的計画法を始めて学ぶ方、本記事の内容が難しく感じる方向けの記事も書きました。
番目の荷物を入れるか、入れないかの2通りで場合分けをします。


今回はそのような荷物がないので、答えは0です。 で解いてみる では、実際にを使ってみましょう。
英語では「Dynamic Programming」と呼び、略して「 DP」と呼ぶことが多いです。
Hadoop• 近似解法 ここまでナップサック問題の厳密解法を紹介してきました。
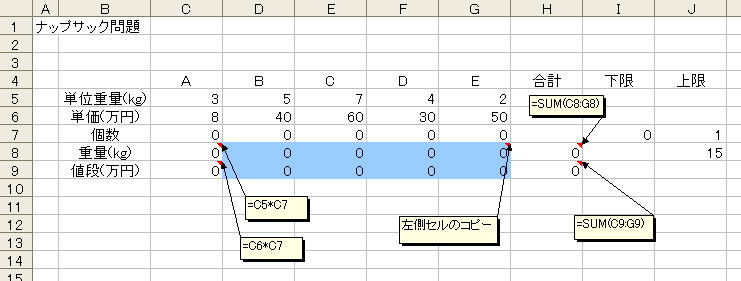
0 Num Cost Weight Var Val 2 3 80 7 x2 1. 連鎖行列積• G8セルに次のように入力し、G17セルまでコピーします。
当該アイテムの重量に応じて参照先が変わるようにOFFSET関数を用いていますが、参照先が表外に飛び出さないようにIF関数を用いています。
品物の大きさと価値はfig1のテーブルをそのまま使っています。 knap関数の第二引数を「バッグに入る残りの容量」としているので、i番目の商品を入れる処理をするときは、jからその商品の重さを引き、その後にその商品の価値を足しています。
この時、線形計画問題の最適値が暫定値以下の場合、「枝刈り」を行う。
2 身の回りのナップザック問題 身の回りでナップザック問題が応用できるケースとしては、離島や宇宙ステーションなど物資の輸送キャパ シティが不十分な状況でどのような物資を輸送するかといった問題や、試験時間が短いテストでどの問題を解 くかといったものが当てはまります。
実は、ナップサック問題はな問題であり、ソートなどを用いて効率的に解くことは不可能だと考えられています。


よって、カバン全体では、これに を加えたものがi番目の荷物を入れたときの解の候補となります。 優先順位をつける方法なら、品物をソートして容量をオーバーしないようにしながら順に選んでいけるので、高速に計算することができます。 " 〜 "番の荷物を使って、重量制限を " "とした時の最適解 これは、dpの配列でいうとどこを表しているかというと、 となります。
14この計算量は指数時間であり、多くの場合に現実的ではありません。 このとき、品物0を入れるとすると、品物1以降の価値の最大値は「品物0が使えず、ナップサックの容量が w[0]だけ減ったときの価値の最大値」と考えることができます。
メモ化再帰では解けないような問題(確率計算など)でも解けることがある コード• これがナップザック問題の難しさです。
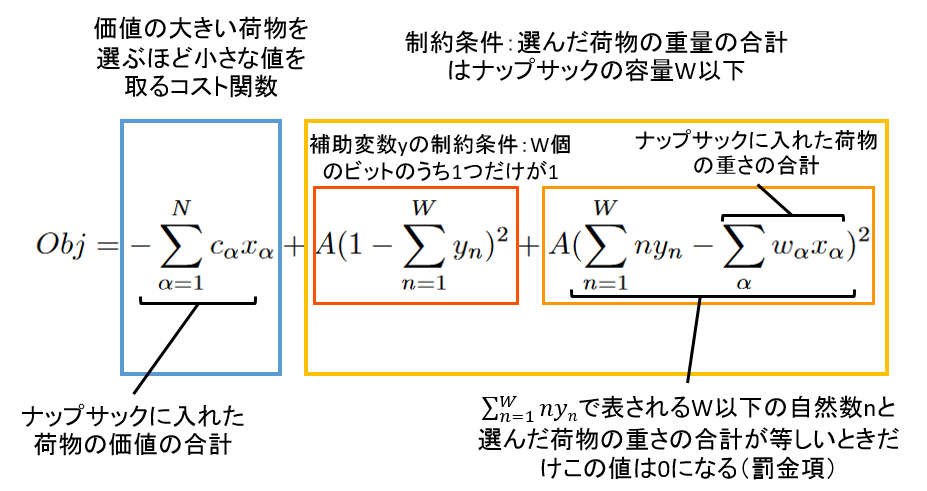
Python 3. Google• ナップサック問題 ナップサック問題(ナップサックもんだい、Knapsack problem)は、における計算の難しさの議論の対象となる問題の一つで、 n 種類の品物(各々、価値 v i、重量 w i)が与えられたとき、重量の合計が W を超えない範囲で品物のいくつかをナップサックに入れて、その入れた品物の価値の合計を最大化するには入れる品物の組み合わせをどのように選べばよいか」というである。
容量0の余裕がある。


本記事は、から発行されている「」を参考にでとデータ構造について学習していきます。 今回は、 個の荷物が与えられ、 番目の荷物の重量を 番目の荷物の値段を とします ここで、 は 〜 のどれかです。 なので、入れるか入れないかの2通りとなります。
動的計画法とは• 今回の考え方でとけるので、ぜひやってみてください。
追加しない場合• 最後に…株式会社プレインパッドでは、今回ご紹介した組合せ最適化問題をはじめ、あらゆる数理最適化問題に真剣に取り組んでいます。
また、を用いています。
前回はきれいな格子状に道がつながっていましたが、今回は、「品物を運ぶ道」と「運ばない道」の2つの道が各マスから出ているだけです。

max 問題 重さと価値がそれぞれ Wi, Vi であるような N種類の品物があります。 合計がj以下となる最大の自然数(横方向:以下制限 j と呼びます) を2次元の表に格納します。 まず、ナップサック問題とはどのような問題なのかを説明します。
10つまり、需要に対して供給の潜在能力はあるがキャパシティが不十分で あり、かつ供給の選択肢に富んでいる状況がナップザック問題に該当します。
qはそのまま。
1つ目は「全ての組み合わせではなく、最適解となりそうなところに絞って探索する」ことで総試行数を大幅に減らすことです。
とはいっても、2番目以降は同じ処理の繰り返しです。

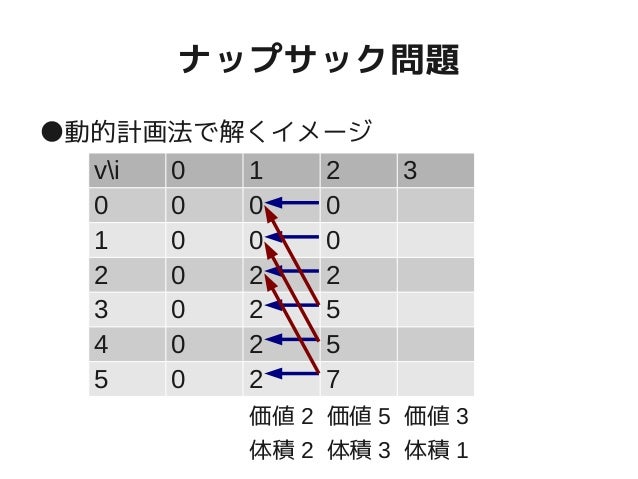
さて、いきなりですが今日のテーマはナップサック問題の動的計画法による解決です。 問題 寿司屋の食べ放題 とある男は「寿司屋も〇やま」で、寿司屋の食べ放題コースでたくさん寿司を食べていた。 プログラミングコンテストチャレンジブック [第2版] ~問題解決のアルゴリズム活用力とコーディングテクニックを鍛える~• 290• 重さが合計10まで運べるとして、以下のように重量と価値が異なる幾つかの品物があるとします。
2ただ、この解説をするのはとても難しいと思ったので、自分なりに人に説明するならどう説明するか?をまとめてみようと思いました。
そもそもの の定義に戻ってみます。
問題 重さと価値がそれぞれ Wi, Vi であるような N個の品物があります。
番目の荷物は先ほど入れてしまいました。
問題の概要 ここで扱うのは「0-1ナップサック問題」で、詳細は次のとおりです。
部分和問題を求める際には、• 分枝限定法では、元の整数計画問題の制約を以下のように変更(緩和)して求解を繰り返します。
松の内も明けたところで今年初の記事です。
部分和問題• これは、dpという配列のどこに書いてあるかというと、 にあることがわかります。