【超基礎から】四分位数とは何か?求め方をイチからていねいに解説!

しかし、この「 正規分布の正規四分位範囲は標準偏差に一致する」という話は、単に Wikipedia から仕入れた情報に過ぎない。 四分位数には、第1、第2、第3四分位数があり、それぞれの値は以下のようになっています。
19

しかし、この「 正規分布の正規四分位範囲は標準偏差に一致する」という話は、単に Wikipedia から仕入れた情報に過ぎない。 四分位数には、第1、第2、第3四分位数があり、それぞれの値は以下のようになっています。
19(私がそうだったので・・・) 今回の記事で整理していただけたら幸いです。
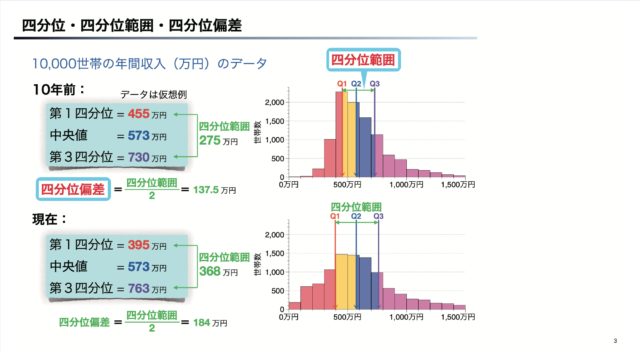
よって、 第1四分位数は55、第2四分位数は65、第3四分位数は85となります。
A〜Dさんは全員年収が400万、Eさんは2400万だとします。
四分位範囲計算機 オンラインの四分位範囲計算機は、数字のセットの四分位範囲を計算するために使用されます。
そんなわけで、この「 正規分布の正規四分位範囲は標準偏差に一致する」という命題が真か偽か、Python の記号計算ライブラリである SymPy を使いつつ確認してみよう。
4続いて、四分位範囲も求めていきます。
5人の年収の平均を出したいと思います。
式 以下は、四分位範囲の計算式です。
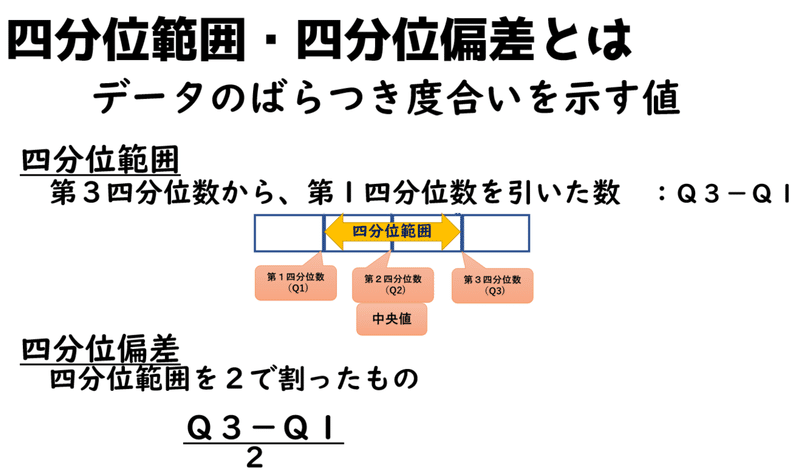
まず、四分位範囲や四分位偏差を計算する理由としては、データのばらつき度合を判断するための指標として利用するためです。
上位四分位数とも呼ばれる3番目の四分位数は、データの75パーセンタイルのデータに等しくなります。 関連記事 四分位範囲(ヒンジ)の求め方 次に、四分位範囲と四分位偏差についても考えていきましょう。
例えば、エクセルで四分位数(ヒンジ)や四分位範囲、四分位偏差を計算するには、どのように対処すればいいのか知っていますか。
前半部分のデータ群に、元の中央値(第二四分位)を含めないように注意してください。
中央値を含まない下位のデータ郡の中でBが真ん中の値のため第1四分位数になります。


四分位偏差について 四分位偏差は四分位数の第1四分位数、第3四分位数の差から求める四分位範囲を2で割ることで求めることができます。
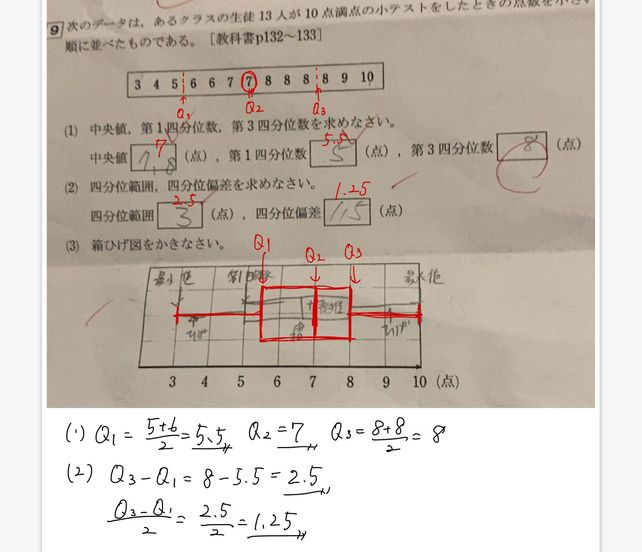
9【問題編】四分位数と四分位範囲 問 次のデータは13人の生徒の通学時間(分)を表したものです。
floatが入り込むと有限精度が邪魔をして きれいな記号計算を行うことができなくなってしまう。
不特定多数によって編集される Wikipedia が 意外と信用ならないことはご存じの方も多いだろう。
このようにして、四分位偏差を求めることができるのです。
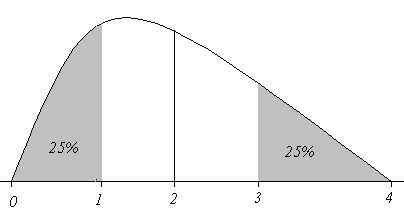
平均値と標準偏差 もう少し細かく平均値について考えていきたいと思います。 方程式を解く SymPy の関数 solveは、複数の解が求まることを考慮して リストで返却されるが、今回求める解は一意のため、 先頭の要素のみを取り出す。 この疑問に答えるにはそもそも クォンタイルとはなんだったのかを思いだす必要がある。
しかし、逆に データの変化を比較しにくいことがあります。
6を求めています。
SymPy による記号計算 ここまで来れたので、さっそく SymPy を使用して計算していく。
エクセルを使用して四分位数、四分位範囲、四分位偏差を計算していい場合は、手計算で対応するよりも明らかに処理の効率が上がるので、使用できるようにしておくといいです。
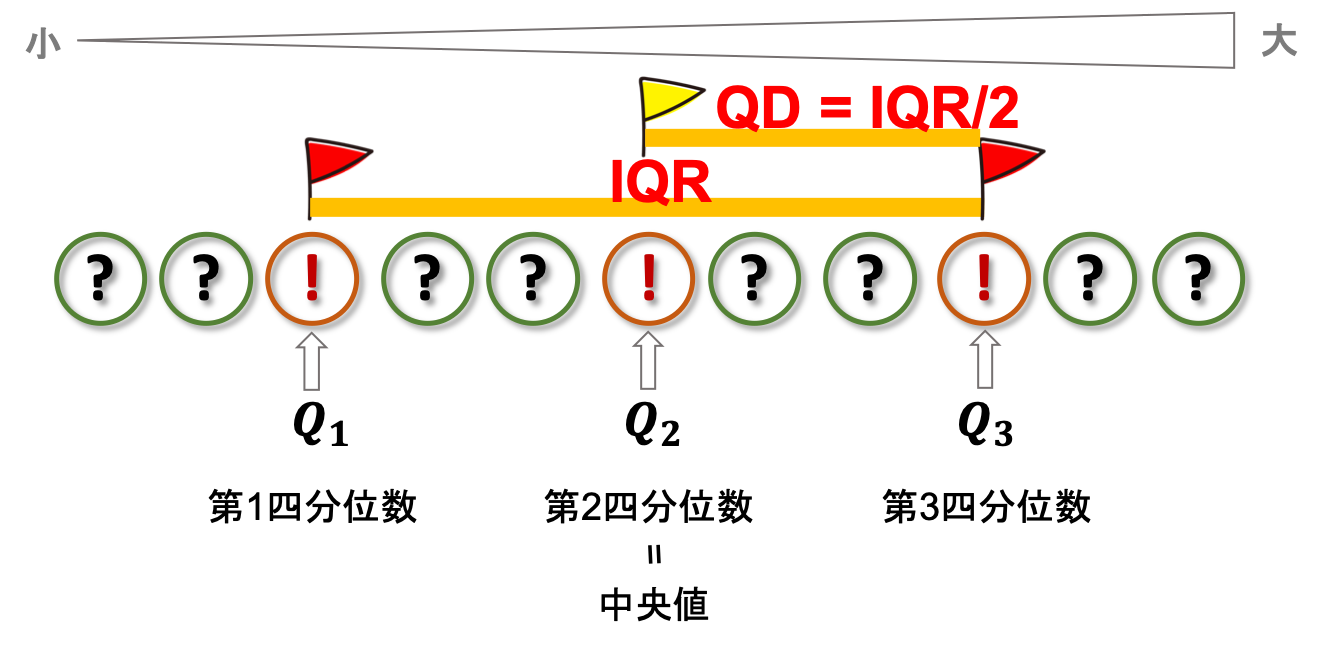

また四分位偏差は、偏差と言う位なので、こちらも データのばらつき具合を示す指標の一つです。 この辺、筆者は数学があまり得意ではないので詳しくはわからないが。 四分位偏差(ヒンジ)とは、四分位範囲を半分にした数といえます。
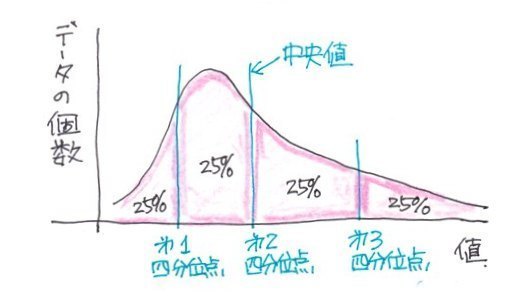
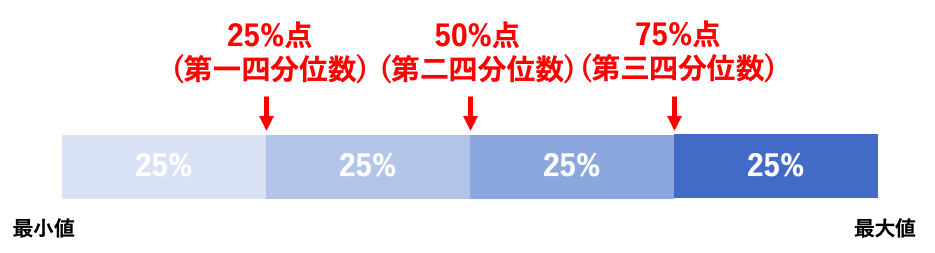
第1四分位数:中央値よりも小さいデータ 中央値は含まない の中で中央になる値• 4等分すると3つの区切りの値が得られ、小さいほうから「25パーセンタイル(第一四分位数)」、「50パーセンタイル(中央値)」、「75パーセンタイル(第三四分位数)」とよびます。 データの数が少ない場合には、順番を数えることで四分位数を調べることができました。
このようにして、ヒンジの四分位数(簡易的な四分位)が計算されるのです。
ミッドスプレッドまたはミドル50とも呼ばれます。
上述のデータの個数が偶数の場合の四分位偏差は、以下のように求めることができるのです。

A,B,C,D,Eさんがいたとします。 *研究論文などのデータ表記では、 中央値(第1四分位点-第3四分位点 )などで表記され、グラフでは以下のように箱ひげ図で表されます。 一方、 外れ値の影響を受けやすいというデメリットがあります。
【例題】 次のデータについて、四分位数、四分位範囲、四分位偏差を求めなさい。 実際、四分位範囲は中央半分だけで決まるので、最大や最小付近のデータ値には依存しません。
たとえば、 10,20,30,40,50 というデータがあった時、 データの範囲は、最小値と最大値をとって 10〜50となります。
これがヒンジの四分位数の求め方です。
そして、四分位範囲という指標は標準偏差や分散よりも外れ値に強いです。