【電磁気学】第06講 ベクトル代数③-三重積

.( 1 2 3 4 5応用 ) 2.( 1 2 3 4 5 ) (5)応用 前節の成分表示を用いて、幾つかの重要な結論が導かれます。 ベクトル A、 B、 Cを下記の様なものだとする。 今、上図の様な、ベクトル Bと Cを含みベクトル Aに平行な面を持つ 平行六面体の角柱OBDCAEGFを考える。 この稿では文章中で ベクトルを表すときには 太字のアルファベット文字を用いることにする。
6
.( 1 2 3 4 5応用 ) 2.( 1 2 3 4 5 ) (5)応用 前節の成分表示を用いて、幾つかの重要な結論が導かれます。 ベクトル A、 B、 Cを下記の様なものだとする。 今、上図の様な、ベクトル Bと Cを含みベクトル Aに平行な面を持つ 平行六面体の角柱OBDCAEGFを考える。 この稿では文章中で ベクトルを表すときには 太字のアルファベット文字を用いることにする。
63番目の公式は : Jacobi Identity であり、1番目の公式より明らかである。 ベクトル三重積の公式 レベル1~2 証明 真面目に成分で計算する方法と、レビチビタ記号を使う方法の二つで証明します。
[] このとき、この成分表示で示されるベクトルの大きさが、実際にベクトル Aとベクトル Bが作る平行四辺形の面積である事は直ちに確認できる。
また(3)が成り立つことはベクトルのスカラー倍の意味と、外積の定義より明らか。
つまり演算の順序が異なると、その結果を表すベクトルの方向は逆転する。
Gibbs, Josiah Willard; Wilson, Edwin Bidwell 1901 , , Scribner , 関連項目 [ ]. .( 1 2 3 4 5 ) 2.外積( 1定義 2 3 4 5 ) 2.外積(ベクトル積) 外積についても、内積と同様な手順で説明できます。
スカラーとベクトルの外積を取ることは出来ないからだ。
また、これが成り立ては Aと Bは互いに垂直です。
この稿では、最も簡単な左端の表現を用いますが、普通の掛け算演算と混同される恐れが在る場合には中央あるいは右端の表現を用いる。

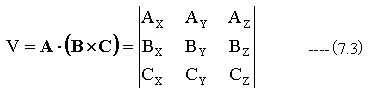
北野正雄『マクスウェル方程式 電磁気学のよりよい理解のために』サイエンス社、2009年2月。 鏡像変換 [ ] スカラー三重積は平行六面体の有向体積を与えるが、有向体積はに対して符号を変える。
[] 上記平行六面体の体積をVとすると、その2乗V 2は となる。
上記の二式と内積、外積の交換法則により、[ A,B,C]の任意の二つの順番を入れ替えると符号が変わることが解る。
通常のベクトルである1-ベクトルが向き付けられた であるように、2-ベクトルは向き付けられた であり、3-ベクトルは向き付けられた である。
そのため上記の式とベクトル i との内積 は前述の平行四辺形をyz平面へ射影した図形の面積となります。
丸山祐一、喜多義範『理工系 ベクトル解析』共立出版、2003年9月。
このとき前項と前々項の結論を用いれば が成り立つ。
このときベクトル A、B、Cの順番はサイクリックに回さなければならないことに注意。
2番目の公式は1番目の公式とクロス積の反対称性から導き出せる。
外積 [ ] 3-ベクトルは有向体積である。 [ Previous: ] [ Up: ] [ Next: ]• 3重積 ベクトルの外積は2つのベクトルから新たなベクトルを創る演算であるから、そのベクトルと新たなベクトルで内積や外積を計算する 3重積(triple products)を構成することが出来る。
スカラー三重積の公式 レベル1~2 証明 真面目に成分で計算する方法と、レビチビタ記号を使う方法の二つで証明します。
ベクトルを扱う大学物理では、外積や内積に関する公式を使って、計算を進めることが多々あります。
それぞれの系は鏡像変換を含まないでは互いに移ることはできない。
スカラー三重積が正となる 付けられた 、もしくはそれから生成される、をとよび、負となる標構を左手系とよぶ。 3つのベクトルの積の演算のうち, と は,電磁気学でしばしばあらわれる.前者をスカラー 3重積,後者はベクトル3重積と呼ぶ.ここではこれらのベクトルの演算について述べる. の演算結果はスカラーになる.まず括弧内の 外積 はベクトルになり,それとベクトル との内積はスカラーにな るからである.そのため,スカラー3重積と呼ばれる. スカラー3重積 は,括弧を省いて, と書かれることもある.この場合でも,ベクトル積 の演算を優先する. の演算を先にすると,こ れがスカラーになり演算を続行することが不可能となるからである. スカラー3重積の性質をカーテシアン座標系で確かめる.成分で表したスカラー3重積は, 32 33 が得られる.明らかに,括弧の位置で演算結果が異なる. ベクトル3重積の証明は,諸君の課題とする.カーテシアン座標系で右辺と左辺の成分を 計算して,等しいことを示せばよい.カーテシアン座標系で成り立てば,他の座標系でも 同じように成り立つ.なぜならば,式 は,ベクトルなので 座標系に依存しない量になっているはずであるからである. ベクトル3重積について,簡単に幾何学的な考察を行う.ベクトル積 の演算結果は,ベクトル にも にも垂直の方向を 向いている.それと とのベクトル積もまた垂直になる.これから,ベクトル3重 積の の方向について,て次のことが言える.• もし Cが Aと Bが作る平面に対して図の反対側にあれば、スカラー三重積の値は負になる。
そのため上記の関係は以下のように変形できる。
以下、 a と b が平行でないとする。
この関係式はとても重要です。

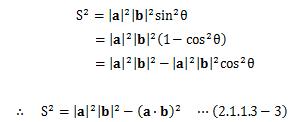
ここでベクトル A、B、Cは互いに右手回りのサイクリックな関係になっていることに注意。 そして普通 などで表す。
また、以下の性質が成り立つ。
これは行列式 に等しい。
左辺・中辺・右辺、どれも図1. 参考文献 [ ]• この稿では、最も簡単な左端の表現を用いますが、普通の掛け算演算と混同される恐れが在る場合には中央あるいは右端の表現を用いる。
ベクトル と が作る平面内にある.• 特に 剛体の力学を論じるとき必須の公式となります。
スカラー三重積の公式 これを示すために右辺を成分記法で書き直すと, 右辺で を順繰りに並べ替えればLevi—Civita記号の符号は変わらずに示したい残りの2つの結果を与える.たとえば, である. スカラー三重積の意味を幾何学的に考えてみよう. 内積の性質からベクトル と のなす角を とすると . 外積の大きさ はベクトル と が作る平行四辺形の面積に等しい. また は位置ベクトル から平行四辺形に下ろした垂線の長さに等しい. したがってスカラー三重積 は3つのベクトルが作る平行六面体の体積に等しい. 平行六面体はどの面を底面としても同じ計算方法で体積が求まることを上の公式は示している. スカラー三重積の幾何学的解釈 次にやはり3つのベクトル に対して という演算を ベクトル三重積という. ベクトル三重積について次が成り立つ:. 内積はスカラー、外積はベクトルなので 外積の持つ性質についてはを参照してください。 つまり が成り立つ。
ところで、別ページで説明する行列式の性質[]と[]から (1)転置行列の行列式は元の行列の行列式の値と同じ。
.内積( 1定義 2 3 4 5 ) 2.( 1 2 3 4 5 ) ベクトルの内積(スカラー積)と外積(ベクトル積)の成分表示 ベクトルの 内積(スカラー積とも言う)と 外積(ベクトル積とも言う)の成分表示を説明します。
幾何学的解釈 [ ] 幾何学的にはスカラー三重積は三つのベクトル a, b, c によって定義されるの のついた を表す。
但し、アルファベットの順番が循環していることに注意しなければならない。 スカラー三重積には幾何的な意味があり、こちらも重要です。
このき、そのベクトルの方向が Aから Bに向かって右ネジを回すとき、ネジの進む方向と同じである場合を で表し、 Bから Aに向かって右ネジを回すとき、ネジの進む方向と同じである場合を で表すことにする。
スカラー三重積が0なら三つのベクトルはであり、 一つの平面に含まれる となる。
なぜなら、体積が0とは平行六面体が潰れていることを意味するからである。