逆行列の求め方~掃き出し法と逆行列の公式の2つの方法の徹底解説~


乱暴ですが、ここでは転置は式をわかりやすくするのに便利で、とりあえずよく行われるものぐらいに覚えておいてください。 それは、以下の行列を左から掛けることと同じことを意味します。 その他の不具合やご要望などがありましたら、おぐえもん()までご連絡ください。
10

乱暴ですが、ここでは転置は式をわかりやすくするのに便利で、とりあえずよく行われるものぐらいに覚えておいてください。 それは、以下の行列を左から掛けることと同じことを意味します。 その他の不具合やご要望などがありましたら、おぐえもん()までご連絡ください。
10これがクロネッカーのデルタです。 ちゃんと調べていないのでわかりませんが、LU分解の演算の数と比べると同じ位になりそうな気がします。
基本行列とは、以下の三つの働きのいずれかを行う行列のことです。
「クロネッカーのデルタ」を使うと、この二つの式を一行で表現することができます。
つまり、それぞれ…• 以上が、掃き出し法で逆行列を求められる理由です。
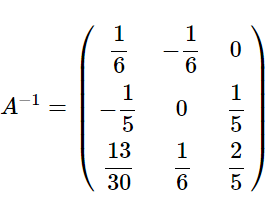

行列の積の逆行列• しかし数学的に考えるという点では逆行列の公式は役に立ちます。 まとめ 以上が逆行列の求め方です。
以上の理由から行列式の値が0になるような行列には逆行列は存在しません。
このようにどちらも同じ値になります。
行列計算機は、行列に関するさまざまな数値 ランク、行列式、トレース、転置行列、逆行列および正方行列など を計算できます。
なお特徴として、逆行列は行列式の値が0以外の行列のみに存在します。

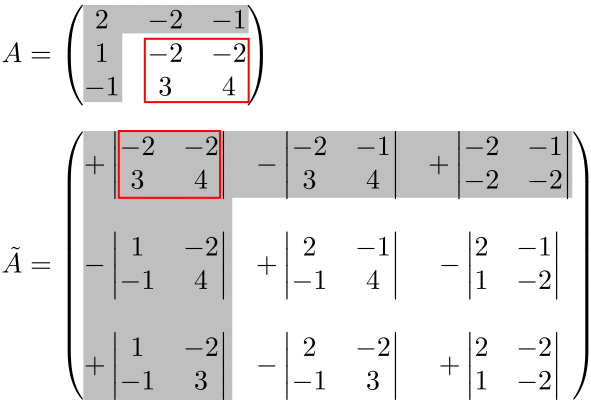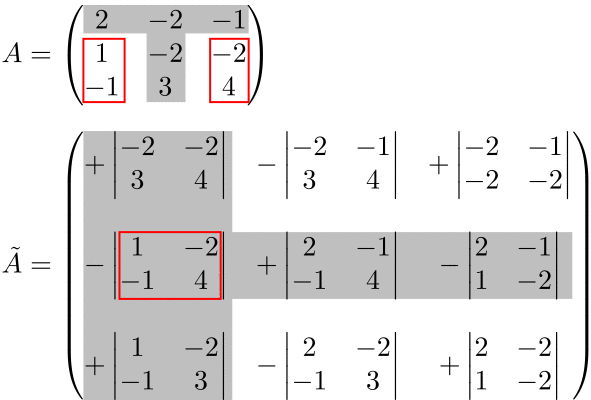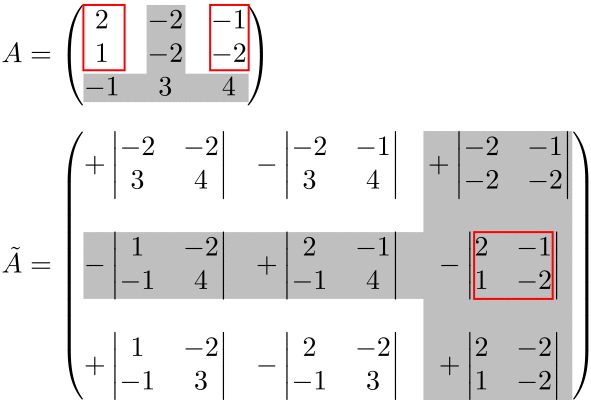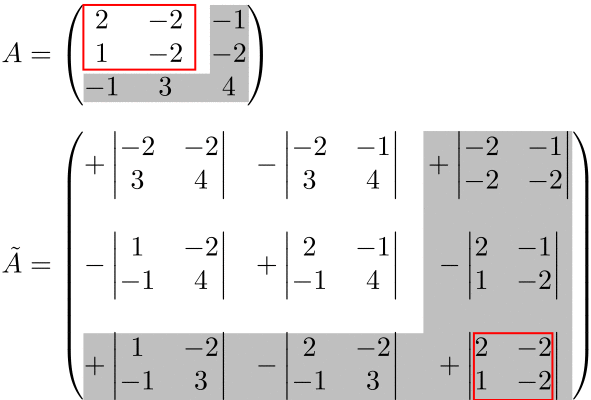
少しでも理解の助けになるように、この点を以下のアニメーションで示しています。
for Turkish translation• それでは始めましょう。 したがって計算例は省略させて頂きます。
カーネル (核・ゼロ空間)は、その行列で線形変換をしたときに、ゼロベクトルに収束する空間のことです。
まとめ 以上が逆行列です。
小数の結果が欲しい方は電卓を叩いてください。
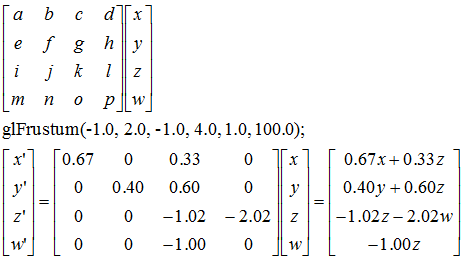
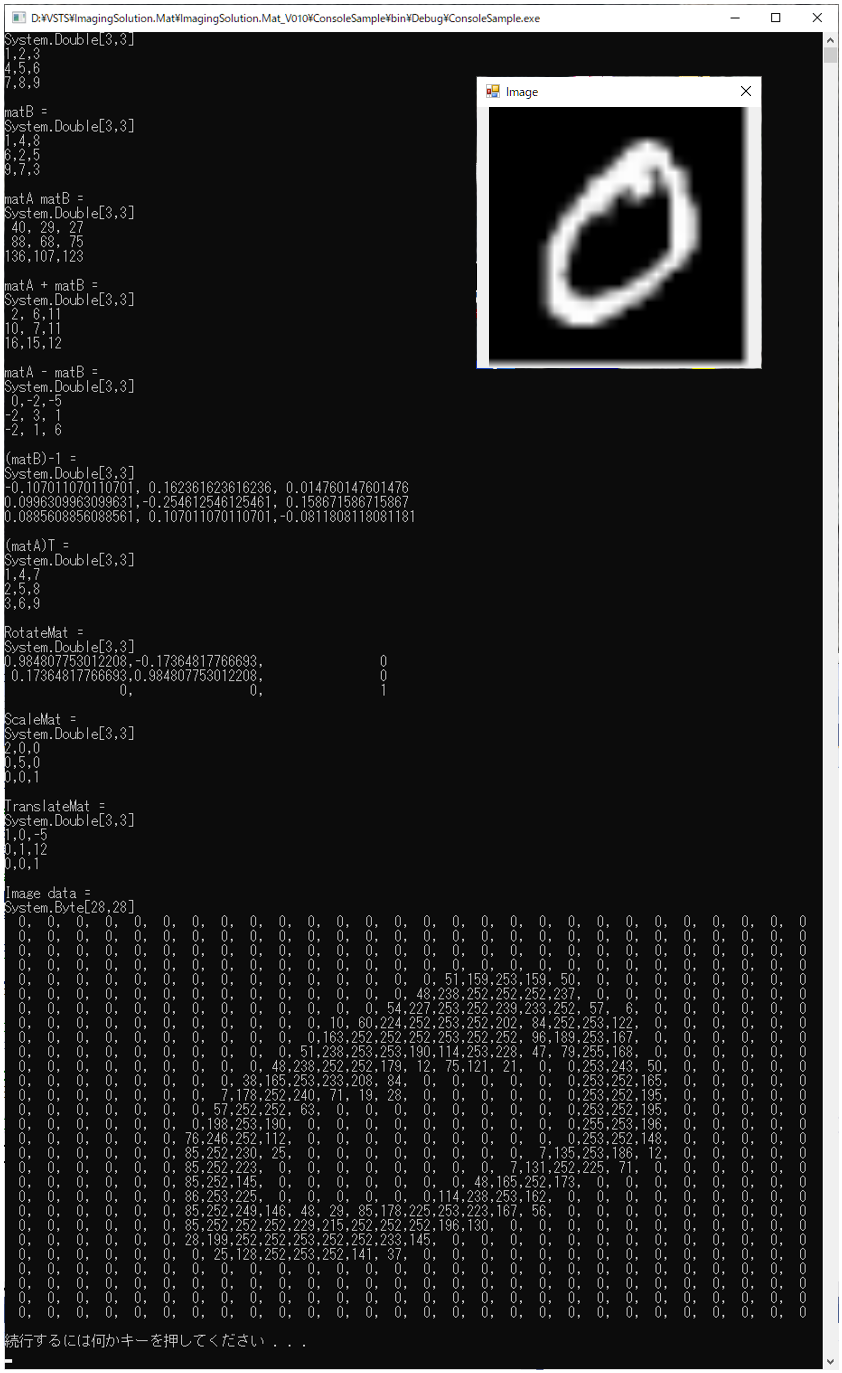
for Macedonian translation• これも行列と逆行列の積は単位行列になることから、以下の式で答えが合っているかどうかを確認することができます。 実際に計算してみると以下のようになります。 入出力は 整数or小数or分数で行われます。
10一方で、逆行列が存在しない行列のことを「非正則行列」と言います。
以上が逆行列の公式の求め方です。
そして、単位行列も転置しても何も変わりません。
Ousama Malouf and Yaseen Ibrahim for Arabic translation•。
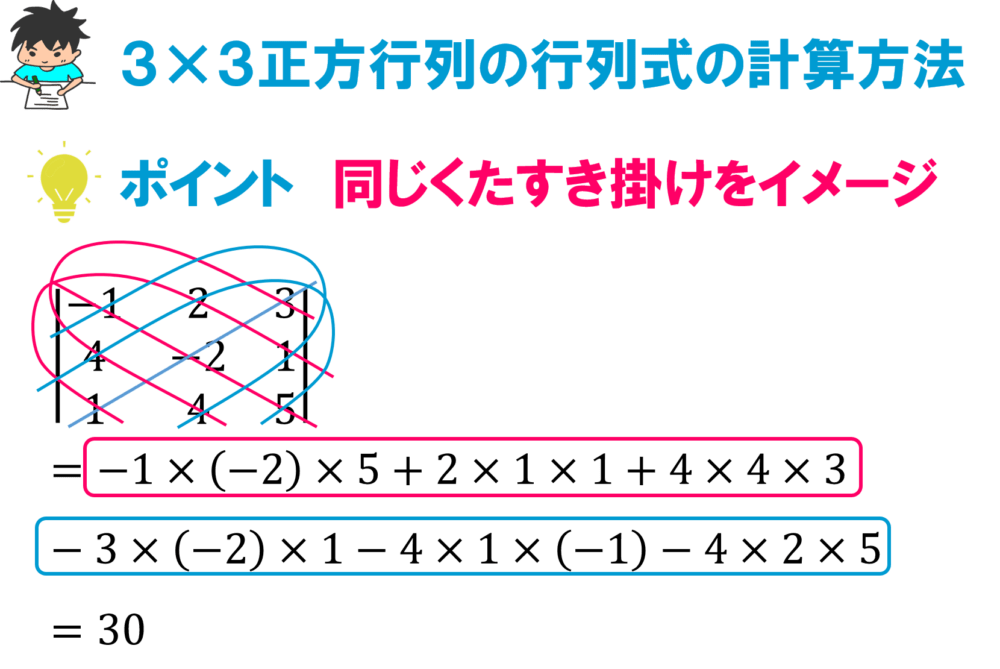
プログラムで行列演算をしていると逆行列が必要になることがしばしばあります。 そもそもこのテの数値演算のアルゴリズムは数式上では正確でもコンピュータに計算させると大きな誤差が発生してしまうので困ったもんです。
20つまり、原因から結果を推測できても、結果から原因を推定できない場合があるということです。
ある行と別の行を入れ替える• ただし、ここの内容は最初は理解できなくても全く問題ありません。
ごちゃごちゃしたプログラムを組まなくても逆行列が出せないかなぁ、と思ってちょっと考察してみました。
もしピンと来なかったとしても問題ありません。
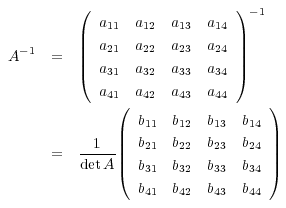

逆行列の性質 それでは最後に知っておきたい逆行列の性質を3つ解説します。 逆行列とは空間を元に戻す行列です。
行列計算機は、40行40列までの行列に対応しています。 行列の階数(ランク)とカーネル(核) さらに深く行列を見ていくと、行列式の値が0の場合にも複数のパターンがあることがわかります。
こうして逆行列を視覚的に理解しておけば、その定義もすんなりと理解できます。
そのため、上述のように実際に逆行列を手計算で求める際は、この逆行列の公式を使うことはありません。
ただし、掃き出し法の方が計算のミスが少ないですし、どのようなサイズの正方行列の逆行列でも無理なく求めることができます。

ただし、実はすべての行列に逆行列が存在するわけではありません。 ルートは未対応…• スカラー倍した行を別の行に足し引きする これらの一つひとつが、基本行列を左から掛けることと同じことを意味します。
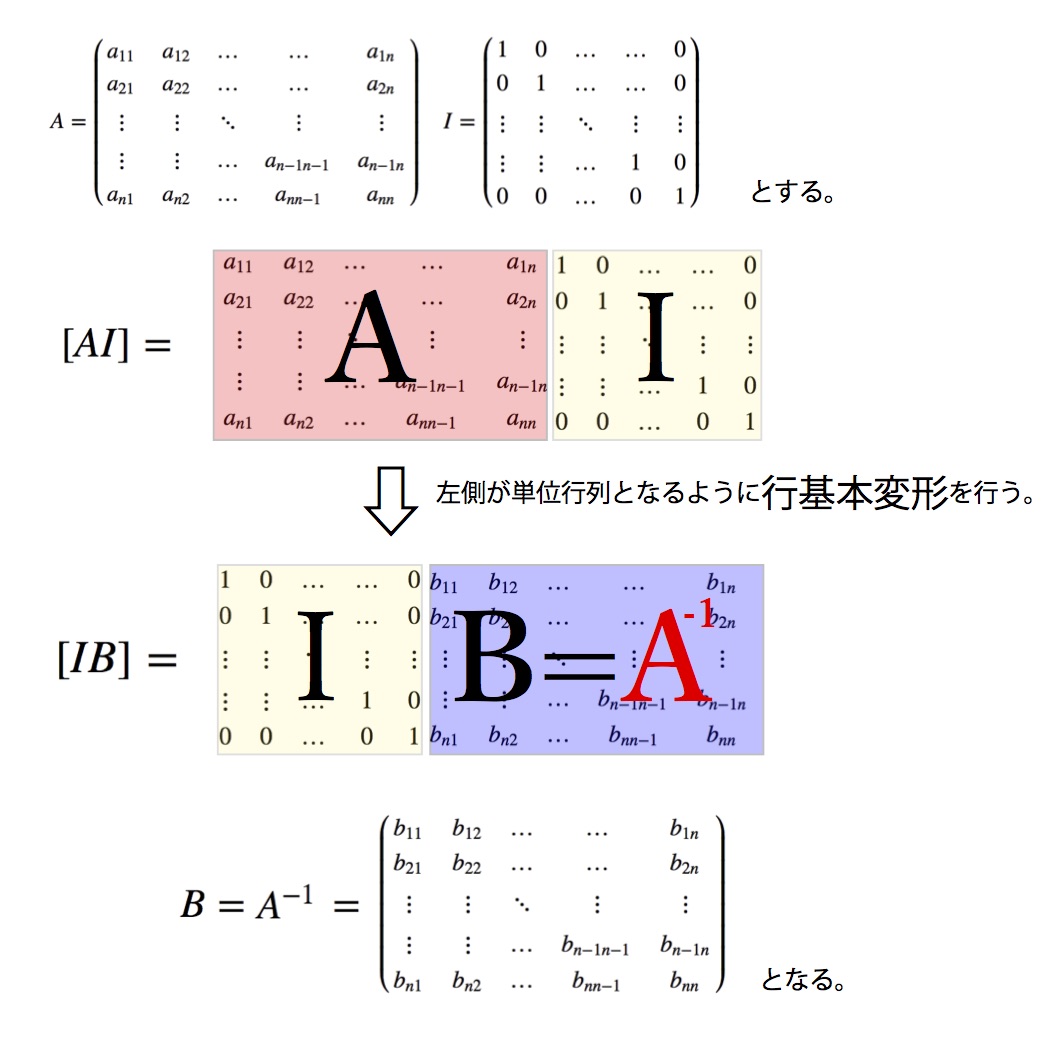
4なぜ、ある行列の右側に単位行列を起き、左側の行列を単位行列に変換したとき、最初に右側に置いた単位行列が逆行列になるのでしょうか。
- fixing the translation into Catalan. これをご覧頂くと、逆行列とは何かを深く理解するための大きな助けとなります。
例えば、以下はPythonのコードです。
逆行列は線形代数において非常に重要な概念ですので、上で解説した求め方や性質・階数やカーネルなどの概念もあわせてしっかりと理解しておきましょう。


消す セル または 共用 挿入 Use decimal keyboard on mobile phones Upload an image with a matrix Note: it may not work well Thanks to:• 理由解説 それでは、なぜこの方法で逆行列を求めることができるのでしょうか。
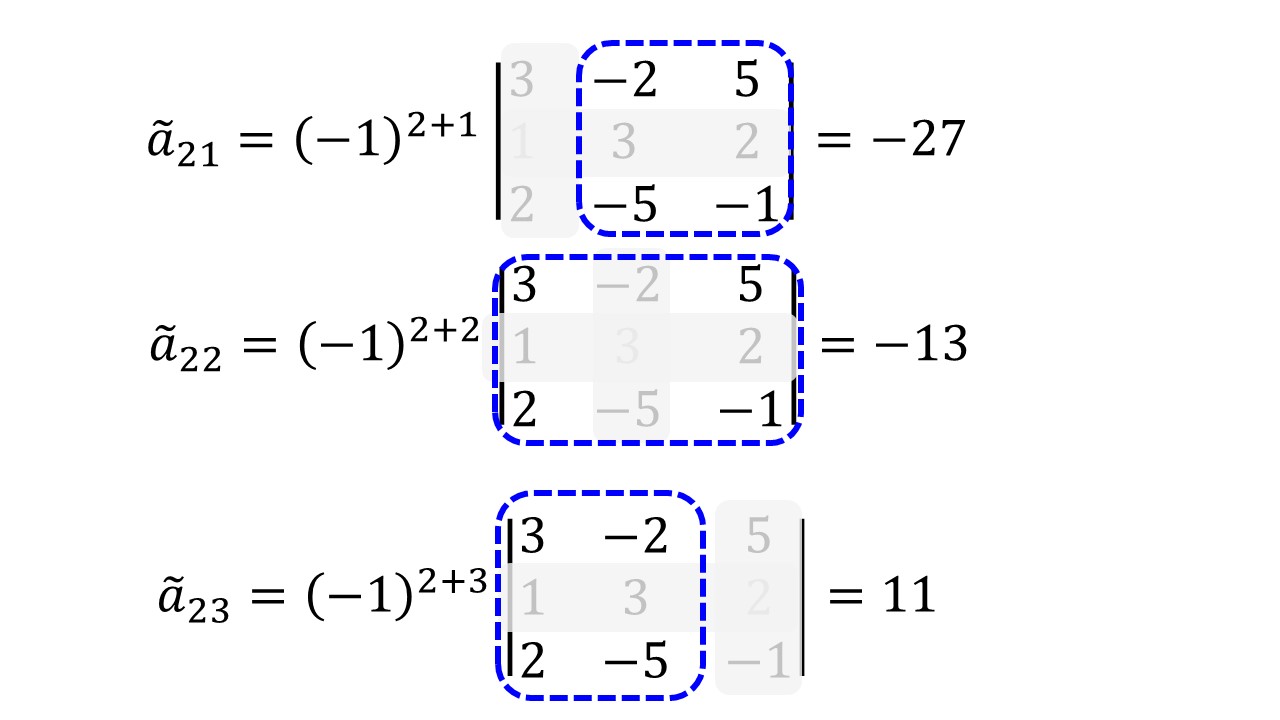
念のため計算方法についても解説しておきます。
行列式の値が0の行列には存在しません。
142rad。
この点については、『』で解説していますので、ぜひご覧になった上で考えてみてください。
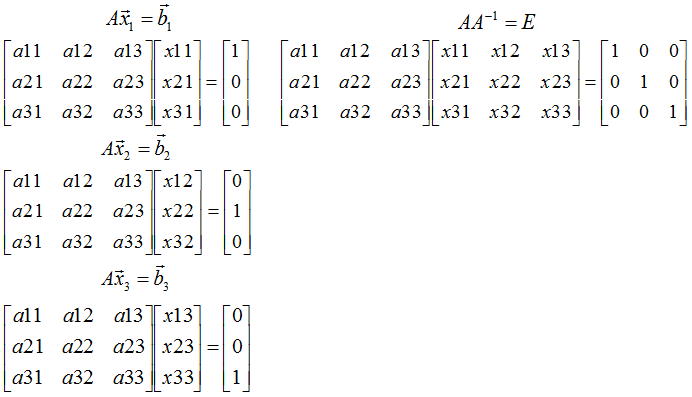

しかし0には何を掛けても0なので、どのような行列を掛けたとしても、もう元の面積である1に戻すことはできません。
逆行列の公式の導出 逆行列の公式を導きだすために、まずは逆行列の定義を思い出しましょう。
スカラー倍した行を別の行に足し引きする このことから、これらの3つの行列は「基本行列」と名付けられているのです。
さあ、これで前置きは終わりです。
逆行列の定義 いきなりですが、以下の短いアニメーションをご覧頂ください。