波動方程式導出。波動方程式とダランベールの公式

Maxwell方程式から、波動方程式=電磁波方程式を導出

流体を表す変数は，圧力，密度，粒子速度，温度，，内部エネルギー等があるのですが，独立している変数は粒子速度 3変数と他の2つだけです。

レーザーを使って微小な動きを測定したり、ピンセットとして原子を掴んだり、もっと工学的な分野では例えば物の切断にも使われています。外力については，まず圧力について考えると，と逆向きに働くのでと書けます。

連続の式媒質が湧き出したり消滅したりすることはないとします。これに対して「波動」は振動する位置も時間とともに動いていく伝搬していくようなイメージです。この音速の式に，実際の固体に応じて数値を入れれば，が求められる。

空気の運動と言うと「」を思い浮かべる方もいるかと思いますがその通りです。

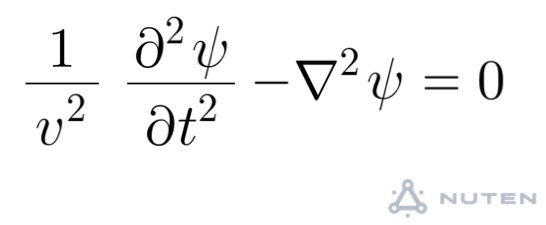
このレーザーの中でも、強度分布が光軸中心から外に向かって次第に減っていくGaussian beamというのがよく使われています。慣性力部分については次のように書けます。

波動方程式とは、「波」を表す方程式で、この方程式の形をとるような場合には空間的に、時間的に波のような性質を持ちます。は3次元空間の位置で，は勿論時刻です。

この状態から，さらにばねをだけ伸ばすと，張力は，になる。つまり、uに関して変化しても一向に構わないのだ。

長さになったばねに改めて座標値を割り付け，そのの部分を考える。これでを導出する準備は完了です。

今風が吹かないような場を仮定すると音による粒子速度はとなります。

以下のような形です。

右図からわかるように，変位の勾配がひずみになるので，位置における力は，となる。目次はじめに現代科学では、レーザーを使うことが少なくない。

参考波動方程式の導出音波は音圧、密度、粒子速度という物理量が密接に関わっています。 Maxwell方程式を受け入れれば、結構、簡単です。

$方程式導出波動$

長さに引き延ばすと，張力はとなる。

そこでではある微小領域の分子の集まりを" 粒子"として，その粒子達の振る舞いを解析します。同様に定常状態の密度をとして，密度変化をとしておきます。

注意点として、ここで扱うのは微小圧力で断熱過程が仮定できる無限小振幅音波の場合で、非常に高い音圧であったり、波長が著しく短い場合は有限振幅音波として扱う必要があります。

ここではと呼ばれるで，以外の変数もに依存する場合に現れます。真空中のMaxwell方程式からの式変形で波動方程式を得るここから、真空中のMaxwell方程式と上記のベクトル演算の方程式を元に、波動方程式を導きます。

Maxwell方程式まず、一般的なMaxwell方程式を下記に記します。
その力は，フックの法則によりひずみに比例している。
固体中の縦波固体中の縦波～波動方程式の導出ここでは，固体中の縦波に対する運動方程式から波動方程式が得られることを示し，さらに音速が密度とヤング率で表せることを示す。

続いて状態方程式、連続の式、運動方程式について考えていきます。

最終的にはGaussian beamを導くのを目的に、まずはMaxwell方程式から波動方程式を導出します。