中3理科「台車の運動」徹底演習!問題のダウンロードも

これを仕事の原理という。 この距離は 全て 0. 力学的エネルギー• 物体の位置が高いほどエネルギーは大きくなる• つまり、斜面を下る運動の場合は、斜面の角度を大きくすると速さの変化が大きくなります。 つまり台車は 一定の割合でだんだん速くなっていきます。
2

これを仕事の原理という。 この距離は 全て 0. 力学的エネルギー• 物体の位置が高いほどエネルギーは大きくなる• つまり、斜面を下る運動の場合は、斜面の角度を大きくすると速さの変化が大きくなります。 つまり台車は 一定の割合でだんだん速くなっていきます。
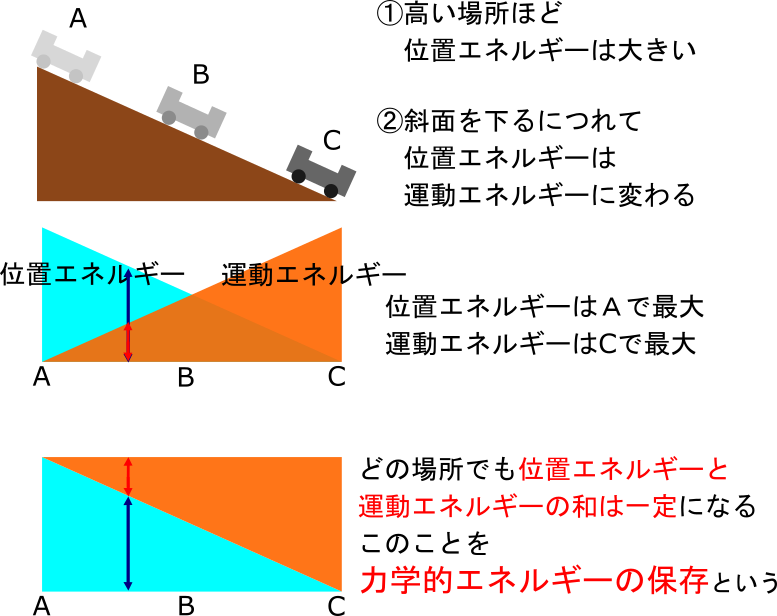
2力の分解 1つの力を2力に分けた力を分力という。 弾性エネルギー エネルギーの移り変わり エネルギー保存の法則 エネルギーが移り変わっても総量は変化しない。
慣性の法則 物体に力がはたらかないときの運動の法則 1. あらゆる方向からはたらく。
光エネルギー• 物体には鉛直下向きに重力 mg がはたらいています。
変換の効率 エネルギーが移り変わる際、すべてのエネルギーが変換されずに一部が熱エネルギーなどになる。

物体の質量が大きいほどエネルギーは大きくなる 運動エネルギー 運動する物体がもつエネルギー• 1秒毎の進んだ距離なので 速さ を表している。 三角比がわかれば、gの向きを斜面方向に分解すればわかりますよね。
7力の合成のパターン• ) 斜面にそった下向きの 一定の力が働く運動となります。 斜面を下る台車の運動(力がはたらき続ける運動)• 物体にはたらく力は斜面を下るときと全く同じであるが、進行方向に対する物体にはたらく力が逆向きなので物体の速さは減少する。
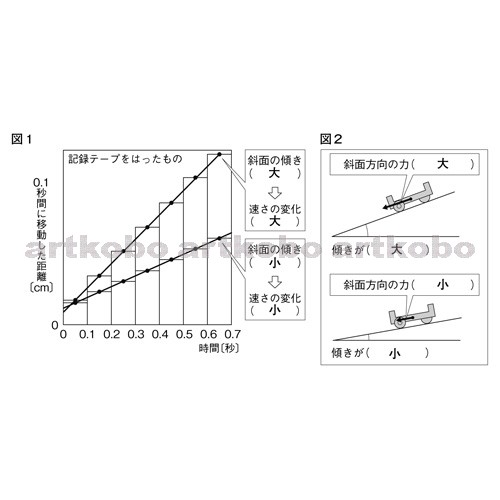
斜面を下る運動 斜面を下る運動のように、進行方向に一定の力がはたらき続ける運動では、次の3つのことがいえます。
速さの増え方は一定で変わらない。
(力のつり合いで学習してください。

1秒毎にグラフの進んだ距離の棒グラフの頂点を結べば直線になっている。 練習問題をダウンロードする *画像をクリックするとPDFファイルをダウンロード出来ます。
9受ける力は 重力であり 傾斜しているので 重力の斜面方向の力を受けている。
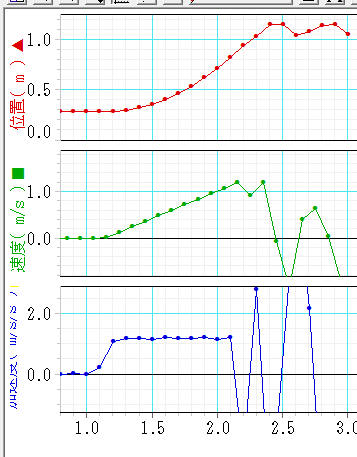
なので グラフは V-tグラフ 速度-時間のグラフ)で 時間当たり一定の大きさで速度(速さが増加している) 速さが増加する=加速度を受けている という事になる。
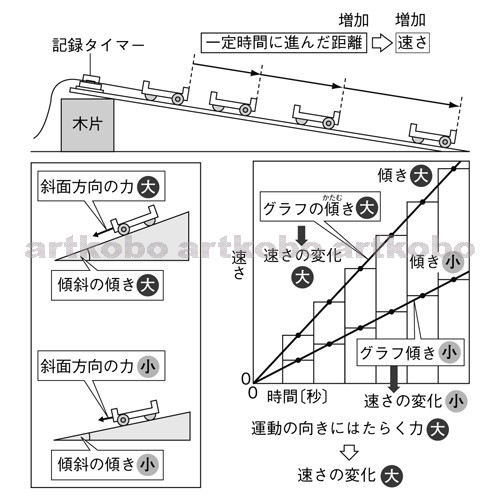
また、角度を固定して、台車を走らせたとき、 台車にはたらく斜面にそう力自体は、斜面上どこでも、同じ大きさの力がはたらいています。
このとき、どれ位の割合で速くなるかを示す値が加速度というものです。
仕事の能率 仕事率 単位時間にする仕事。
音エネルギー• 電気エネルギー• 熱 放射 物体から熱エネルギーが放出されること。
斜面は摩擦の無い面であるとします。
運動方向と運動方向と垂直な方向に分解 物理の演習問題を解くとき、 運動方向と 運動方向と垂直な方向にすることがよくあります。
一直線上で向きが反対• これは物体にはたらく力の合力がいくらかあったからである。
また、この 合力が0のときは速度が変化しないということである。
てこ 支点、力点、作用点の位置によって必要な力と力を加える距離が変わる。
例えば、 mg に沿った鉛直な補助線を引きます。

定滑車と動滑車 動滑車 必要な力は半分になるが、力を加える距離は2倍になる。 斜面による力の分解 斜面では重力が斜面に平行な力と斜面に垂直な力に分解される。
16等速直線運動 一定の速さで直進する運動。 (垂直というのは何かに対して直角という意味で、鉛直というのは重力の方向という意味です。
(例)カーリングのストーン 慣性 物体がその運動を続けようとする性質。
テープの 点の数は 時間を表す。
別のいい方をすれば、力がということです。
2力が同一直線状にある (例1)綱引きで綱が動かない状態 (例2)重力と垂直抗力 (垂直)抗力 面の上に物体を置いたとき、その面から垂直にはたらく力 摩擦 まさつ 力 物体の運動をさまたげる力 力の合成 2つの力と同じはたらきをする1つの力を2つの力の合力という。
つり合っているのでこの方向には物体は動かないので、今この方向に関しては何も考えません。
) 台車に加わる力は一定、ということは、その台車には、常に同じ力(重力による力)が加わっているわけですね。
自由落下運動のように力がはたらき続ける運動です。

重力を斜面を垂直に押す力と 斜面にそった下向きの力に分解することができます。 作用・反作用 作用・反作用の法則 物体に力を加えると物体からも力を受ける。
水中に沈んでいる体積が大きくなるほど、浮力は大きくなる。
それぞれの運動のまとめ 等速直運動のグラフは 斜面を下るor自由落下のグラフは となる。
時間と移動距離の関係 速さが一定の割合で増加するので、距離は時間の2乗に比例する 放物線になります。
2力の大きさが等しい• 分力を求めることを力の分解という。