什么是既约分数?_百度知道

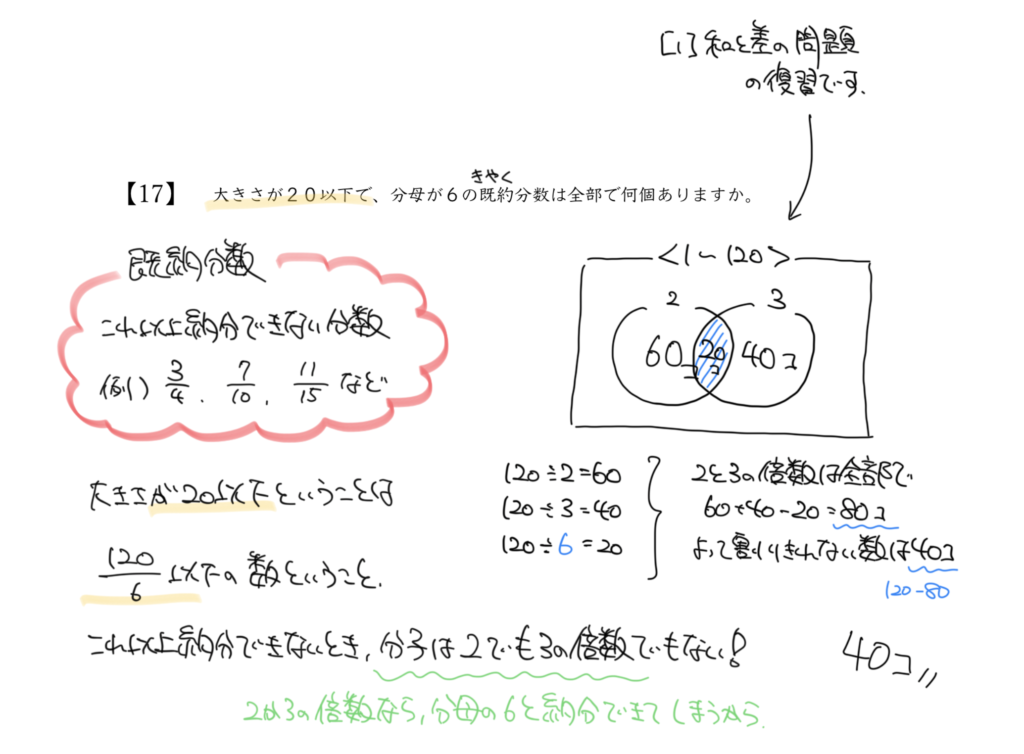
既約分数の定義 既約分数の定義を下記に示します。 从而使得学生明显个性色彩的想法和思维得以暴露。


既約分数の定義 既約分数の定義を下記に示します。 从而使得学生明显个性色彩的想法和思维得以暴露。
無限小数の詳細は、下記が参考になります。
2、分数中的分子或分母经过约分后不能出现无理数(如2的平方根),否则就不是分数。
上記の分数は、分子と分母に1以外の公約数がありません。
TotalMinutes ; あなたの例で示した文字列のいずれかを valueとして渡すことができ value。


4で計算する事になりますが、 この辺り分子の44、45、46がすべて「約分できる」ので、 「答えには入らない」と判断できるからです。 展开全部 既约分数即最简分数。 既約分数は、これ以上、約分できない分数のことです。
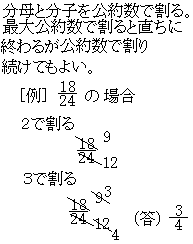
161 倍分(分母と分子に同じ数をかける)して、条件の数字に揃える 「条件」は「24を分母とする分数」ですので、倍分して分母を24にします。 既約分数式ともいいます。
既約分数と公約数の関係 既約分数は、分子と分母に1以外の公約数がない分数です。
这一做法不仅有效地调动了学生学习的积极性,转变学生的学习方式,而且充分注重了知识结论的动态生成过程。
3、分数的分子和分母为互质数的分数叫最简分数。
ここでは、条件ロジックと、リード評価を返す ISPICKVAL 関数の両方を使用する数式を記述します。 例子: 例1. Electrical 電気関係 のケースには優先度 1、Electronic 電子関係 のケースには 2 などのように指定します。
[エラー条件数式] に、次の入力規則を入力します。
是最简分数 解:8 和 21 是互质数,所有 是最简分数。
要は、受験の現場では「正解が出せれば良い」わけですから。
既約分数と公約数の関係 既約分数は、分子と分母に1以外の公約数がない分数です。
。 既約分数と既約分数式 既約分数と既約分数式は同じ意味です。
最简分数的分数的分子与分母没有除1以外的其他公约数。
違いを理解しましょう。
参考资料: 是最简分数 解:8 和 21 是互质数,所有 是最简分数。
下記が参考になります。
「高校の時は、物理が苦手で」「計算ができなくて」といった言葉が次に続き、次第に僕との距離が広がっていく。
可以从创设问题情境开始,让学生历经感受、猜想、例证、感悟等过程。
想法的正确与否是次要的,重要的是学生有机会表达自己对新知识的最真实的感受与理解,这些想法为学生进一步抽象出最简分数的本质提供了宝贵的资源。


1、约分:把一个分数化成同它相等,但分子、分母都比较小的分数,叫做约分。 ポイントは、倍分しても分数としての 割合は変わらない事です。
テーラー展開・マクローリン展開 物理の計算では死ぬほど使うので、めちゃくちゃ使います。
通常要除到得出最简分数为止。
要約や補足を加えたとき、確認や修正の手間を劇的に減らせるので、ぜひ活用してみてください。
最简分数是分子、分母只有公因数1的分数,或者说分子和分母互质的分数,又称既约分数。
公約数とは、2つ以上の整数で共通する約数のことです。
よって、まだ約分できるので既約分数とは言えません。
最简分数,是分子、分母只有公因数1的分数,或者说分子和分母互质的分数,又称既约分数。
よってこれ以上、約分できません。