スターリングの公式とガンマ関数


計算機向けの変形 [ ] ガンマ関数の(関数電卓などの)計算機向けの近似として次の式がある。 ただし、6四半期連続の成長は、日本における10年ぶりの最高水準かもしれないものの、それは他の先進国と比べたところそれほど印象的な活躍ではありません。


計算機向けの変形 [ ] ガンマ関数の(関数電卓などの)計算機向けの近似として次の式がある。 ただし、6四半期連続の成長は、日本における10年ぶりの最高水準かもしれないものの、それは他の先進国と比べたところそれほど印象的な活躍ではありません。
なお、ガンマ関数の値を求めるプログラムを書こうとしたが、すでに奥村晴彦氏による「改訂新版 C 言語による標準アルゴリズム事典」があり、JavaScript で書いてもこの焼き直しに過ぎないので、 諦めることにした。 スターリングの公式の別バージョン スターリングの公式には他にも様々なバージョンが存在します。
, Asymptotics and the Mellin-Barnes Integrals, Cambridge University Press, 2001• Whittaker, E. これがガンマ関数の漸近形であり、スターリングの公式はここからすぐに導くことができる。
。
第2四半期を迎えた日本経済は、個人消費と設備投資が2年以上に亘って最速のペースで成長。

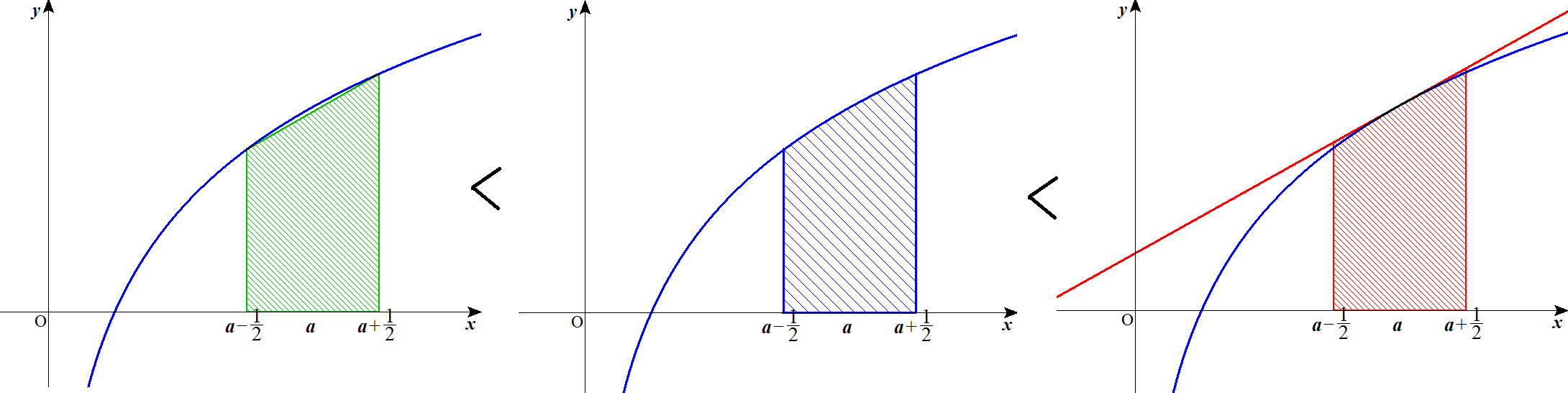
の値についての近似公式であり、 具体的には次の式で与えられる。 この関係式はとくによく使われるので覚えておくとよい。 それではガンマ関数のより正確な近似式を計算していこう。
20以上よりスターリングの公式 [math] n! の間にある。
ガンマ関数は階乗を一般化した関数である。
つまり、日本には働き口が必要なのです。
収束の速度と誤差見積もり [ ] より正確に記すと、次のようになる。

なお、以下の2つの記事の結果を用いるので合わせて参照ください。 Elic W. Programmable Calculators: Calculators and the Gamma Function. > > スターリングの公式 MARUYAMA Satosi. 2002年、Robert H. 4 Stirling's Asymptotic Formula"• この近似は z の実数部が 8 以上のとき、小数点以下 8 桁を超える精度を持つ。
5それにもかかわらず、スターリングの公式をなお適用することができる。
統計力学(物理の一分野)や組み合わせ数学で用いられます。
このような経済の伸びはアベノミクスの産物なのでしょうか?ある程度はそうだと言えるでしょう。
ガンマ関数に対するスターリングの公式 [ ] すべての正の整数に対して、 n! 最後の弛緩期に心筋の長さがどれくらいだったかが、次回の心筋の収縮能力に影響を及ぼす。

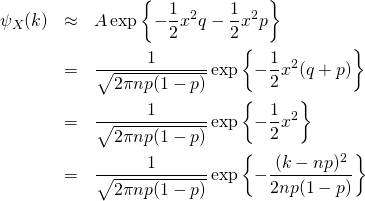
08%にまで減少し,公式による近似がかなりよいことがわかる。 004 です。
収束級数形式のスターリングの公式 [ ] の John Canton への書簡がににより公表されている。 そして、日本の急速な高齢化と労働力の減少という人口学的課題からも目を背けることはできないでしょう。
を示します。
5%だとする兼ねてからの上昇予想を上回りました。
ただし、この法則は心臓の動きか生理的正常範囲内であることを前提にしている。


導出 [ ] 初等的な導出 [ ] スターリングの公式の厳密な証明には、あるいはといった複素解析の技法などを用いられることが多いが、初等的に導くことも可能である。 アベノミクスの議題として、より多くの人々が労働市場に参入できるようにはからうという計画があります。
12確かに、個人消費とビジネス投資の伸びは大歓迎以外の何物でもありません。 これは多量のや振動子についての黒体放射エネルギーの方程式にリンクしている。
ガンマ関数の漸近展開の導出法として一般によく知られている方法では、その計算過程に複数回の近似があらわれるため導出法としてなんとなく怪しいところがあるのだが、このページで紹介する方法ではテイラー多項式による近似を1回用いるだけなので、近似計算として怪しいところがなく、近似の意図も明瞭になっていると思う。
(個人的に、この表式がガンマ関数の最も自然な積分表示だと思っている。
この節ではガンマ関数の基本的な性質について復習するが、すでによく知っている人は次の節まで読み飛ばしてよい。
4%のインフレ率は依然として日本銀行の目標とする2%を大幅に下回っています。 ガンマ関数の基本的な性質 スターリングの公式はガンマ関数の漸近展開から導出される。
スターリングの公式の収束級数形式を得るには以下を評価する。
故に、次によい近似の ()は n! 数式表示 数式表示には を用いている。
008 になります。