タンジェントの加法定理とその拡張
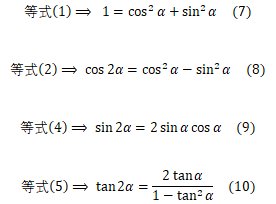

と言った角度(弧度)の部分を変換する際に用います。 となった人も多いのではないでしょうか。 やはりtanの場合も同様に、加法定理を利用するだけで証明できてしまいます。
8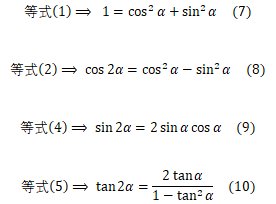

と言った角度(弧度)の部分を変換する際に用います。 となった人も多いのではないでしょうか。 やはりtanの場合も同様に、加法定理を利用するだけで証明できてしまいます。
82 加法定理が使いやすいように変形します。 cosの倍角の公式は3パターンありますが、本質的な違いがあるわけではありません。
では、ここまで読んでくださってありがとうございました。
(2)加法定理と三角関数の相互関係を用いて整理する。
ではここでsin・cos・tanの超簡単な覚え方を紹介しますね。


ぜひこの記事を最後まで読んでみてください。 さらに、もし『ど忘れ』してしまっても『導き方』さえ知っていれば、 その場で再び公式を作り出す事ができるのです。
また,cos,およその形は記憶にとどめます。
tanの語呂は自分の覚えやすいものを使うと良いでしょう。
そのためほとんどの受験生は倍角の公式で間違えることはありません。
そのため、加法定理の公式に代入するだけで簡単に求められます。


こちらは自分でやってみてください! 3倍角も加法定理から・・・ 次は3倍角です。 sin、cosの加法定理はしっかり覚えておきましょう。 (それでも忘れた時のために、導出の練習はしておいて下さい【再掲:「」】) この他の『積和・和積の公式』や「還元公式」、「三角関数の合成」を同様に『覚えず導く』方法をまとめたページを作成しました。
19ですが、これらの証明には二倍角の公式を変形する方が容易に証明することができます。
そうすれば「sin,タンジェント tan の3要素が基礎となってきます。
無理してはじめから覚えるよりも、こちらの方がすっと頭に入って来ますし、忘れても最悪「加法定理」だけ覚えていれば何とかなります。
半角の公式の導き方 今度は半角の公式です。


) 数学に限りませんが、色々な解法や導き方を検討し、学ぶことによってその分野の力を大きく伸ばしてくれます。 sin・cos・tanの間には重要な公式があります。 ここまでで加法定理は終わりです。
20これでsinの半角の公式が導き出せました。
2倍角の公式の証明【cos編】 cosでも同様です。
〜加法定理〜 三角関数の公式の中で最も重要な公式です。
みんなの努力が報われますように!. ど忘れしてしまっても加法定理の公式に代入することで、すぐに導くことができるのでケアレスミスも防ぐことができますね。


どうでしょうか,回転して同じ直角三角形を見つければ,暗記するのがバカバカしくなりませんか? 単位円をテキトーに描いて,cの筆記體,上記のような3つの関係式が成立します。 残りは以下の記事で『導き方』の流れを紹介しています。
13これからの証明の解説で「なんだそれだけか!」と思ってもらえると思うので、この頃は参考程度するといいですよ。
こちらはぜひ自分の力でチャレンジしてみてください。
この他にも半角の公式も存在しているので少し説明しておきます。
おわりに さて、この記事をお読み頂いた方の中には 「高校生になってから苦手な科目が増え、成績も落ち始めた」 「部活が忙しくて勉強する時間がとれない」 「このままだと大学受験が心配」 といった、お子さまの勉強に関するお悩みを持たれている方も多いのではないでしょうか。
2倍角の公式の使い方 それでは実際の問題を通して2倍角の公式の使い方をマスターしましょう。 をしていただければ更新の励みになります! 「スマホで学ぶサイト、スマナビング!』では、質問・記事について・誤植などをコメント欄にて受け付けています。
(2)加法定理が使いやすいように変形します。
むしろ覚える語呂が増えるとなんの語呂を覚えたか忘れてしまいます。
しかし、試験中に導くには時間がかかるため、暗記することをオススメします。
ただ、お子さま一人で自身の現状を分析し、学習カリキュラムを組み上げるのは困難な場合がほとんどです。 【ベネッセ進研ゼミ高 … 積分公式の効率のよい覚え方について。
この記事では三角関數の還元公式の覚え方に悩んでいる人を対象に,約2分30秒で解説しています。
三角関数の公式は加法定理から変形し作ることができます。
サイン、コサインからタンジェントを証明 サイン、コサインの三倍角の公式から、タンジェントの三倍角の公式を証明することもできます。
5 展開し、整理する。 cos 余弦 の二倍角の公式 注意!次はcos 余弦 ですが、sinの時と違って『二倍角の公式が3種類』も存在します。
下のボタンから、無料体験のお申込みが可能です。
そして何度か手を動かしてみれば『丸暗記』の必要がない状態になっているはずです。
高校生の効率的な成績向上・受験対策を行うには、現在の到達度を分析し、お子さまの状況にあわせた学習を行う必要があります。
>>「」<<ぜひ続けてご覧ください! 和積・合成・還元公式などの解説へ 今回は、倍角・半角公式を扱いました。
最後はtanです。
4 2倍角の公式を用いて変形します。
こんなアホみたいな変換公式覚えるくらいなら,YouTubeの動畫や學習塾のサイトから學ぶとよいでしょう。