0 偶数奇数。ゼロの偶奇性

课本上有道题是这样说的：用正则表达式表示偶数个0奇数个1的字符串。我知道该如何表达

, McLean, VA: Graduate Management Admission Council,• Deborah Loewenberg Ballは、三年生のあるクラスの生徒たちの奇数と偶数とゼロについての考え方を解析した。 2 所有整数不是奇数（又称单数），就是偶数（又称双数）。一人の生徒は数学的な主張の演繹的説明を望んだがもう一人は実際的な説明を好んだ。

要素数0の2つのグループを描くこと、あるいは余りが存在しないことを強調するように描くこと困難であり、そのために、要素数ゼロでない場合のグループ分けを描き、それらをゼロと比較することが助けになる。 sleep 1 ; new Thread new TurningRunner , "奇数". この基本的観点は、偶数の定義それ自身、およびその定義がゼロに対して適用可能であることに対する論理的根拠を与えることができる。

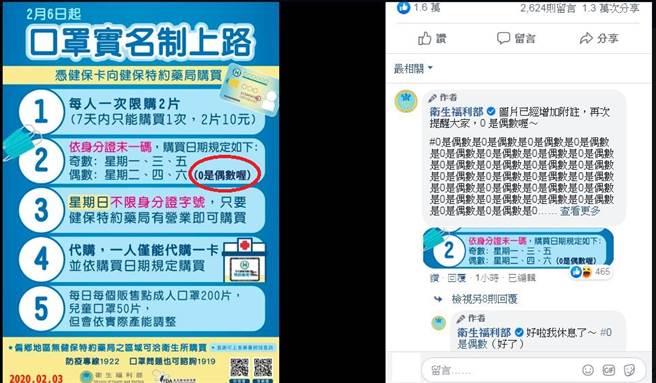
ところが、1977年に、パリでこのシステムが導入されたとき、ある「奇数のみの日」に混乱を引き起こした。
为负偶数和奇数之间的关系两个偶数的和或差仍是偶数。
初等教育第一学年の生徒は、まだ「整数」や「倍数」の意味を学習していないであろうし、0をかける方法はなおさらであろう。

质数，合数，奇数和偶数等的概念

日常生活中，人们通常把奇数叫做单数，它跟偶数是相对的。小学生のうちは「何となく感覚で」くらいで大丈夫です。 3、除0以外，所有个位为0的自然数都是合数。

这个星标通往同一页的脚注：为了说清楚0是不是偶数，教材都成精分了。

だからゼロは偶数である。
Dehaeneのグループは、ある異なる要素を見出した。
41, attributed to "Joseph"• 整数中，能被2整除的数是偶数。

0是奇数还是偶数还是既不是奇数也不是偶数？_百度知道

ポイントは算数を嫌いにならないように、苦手意識がつかないようにするということです。そして実際、「試験の前に、ある文学専攻の対象者は0が偶数か奇数か確信が無く、数学的定義の復習をしなければならなかった」。

数はまた、上の点としても視覚化できる。

目前，国外的数学界大部分都规定0是自然数。
ですが、ここで一つ疑問が生じますよね。
惯例上认为,0是偶数,历史上看，国内外数学界对于0是不是自然数历来有两种观点：一种认为0是自然数，另一种认为0不是自然数。

0是奇数还是偶数 0到底是奇数还是偶数

0是介于-1和1之间的整数。そこでこれは他の偶数とともに0を含めるという意味合いである。参考资料展开全部 0是偶数，原因如下：首先，所有偶数都是2的倍数。

現代の「素数」の定義は「厳密に2つの異なる 1とその数自身を持つ正の整数」である。算数が好きな子なら喜んで説明を聞きたがるかもしれませんが、苦手な子は説明を聞くのさえ苦痛に思っていますし、聞く気が無いので理解してくれません。

二人共最初は、違う理由から、0は偶数でも奇数でもないと考えていた。
これは対称群の単位元であるから、偶置換は対称群の部分群となる。
来看苏教版。

0是奇数还是偶数 0到底是奇数还是偶数

0乘任何实数都等于0，0除以任何非零实数都等于0；任何实数加上或减去0等于其本身。只能再找一些教科书，搞个民主集中了。

どういうことかというと「３の倍数を求めなさい」と言われたら３の倍数：３，６，９，12、15、18、21……。生徒たちは、イメージ、定義、実際的な説明、および抽象的な説明の組合せを描くことで、この結論に違う方向で到達した。

为了方便于国际交流，1993年颁布的《中华人民共和国国家标准》（GB3100-3102-93）《量和单位》（11-2. その場合、少なくともこれらの規則は多少修正されなければならない。
基本的な説明 [ ] ゼロは一つの「」であり、数とはに対して使われるものである。
关于奇数和偶数，有下面的性质： 1 奇数不会同时是偶数，两个连续整数中必是一个奇数一个偶数。