第8章 構造解析法への適用
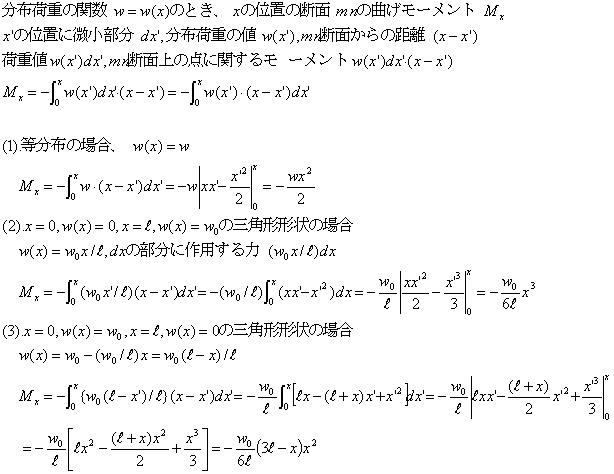
回転軸から力の作用線までの距離のことです。 このてこの原理を発見した人物が、かの有名なアルキメデスになります。
11再度、力のモーメントについて確認しましょう。
今回は簡単に説明しますが、斜めの力は鉛直と水平に分解すれば良いのです。
応力については下記を参考にしてください。
鉛直方向に荷重は作用していません。

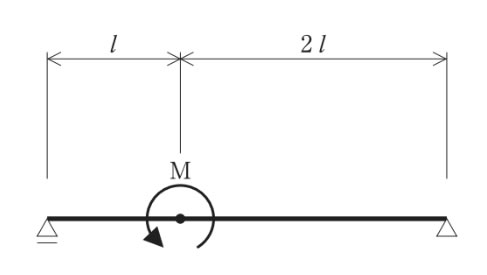
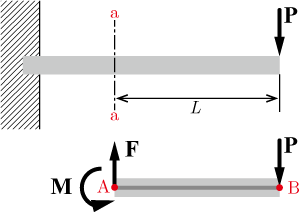
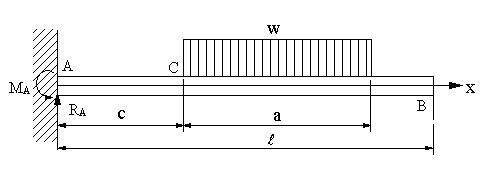
4 応力法による解法 不静定ばりの各種解析法の特徴を理解するため、 1次の不静定ばりである「枕片持ちばり」を例に、支点反力及び断面力を求めてみましょう。 では、軸を倒さないようにするためにはどうすればよいでしょうか?答えは「反対側(右側)に同じ力のモーメントを負荷する」、すなわち、左側と右側で力のモーメントを同じにすれば良い(力のモーメントをつり合わせる)ということになります。
興味のない方はスキップしてもらって構いません。 慣れるまでは毎回、モーメントのつり合いの式を立てて、反力を求めていきましょう。
力のモーメントはトルクとも呼ばれ、はるか昔、てこの原理として経験的に知られておりました。
しかしこれ以外に、慎重に考えなければいけないことがあります。
「Q点を固定して、A点から力を加えると棒は回転する。
シーソー勝負において、同じ体重同士なら外側に座った方が有利です。 取り除いた部分に単位(=1)の不静定力を加え、 静定基本系の変位(たわみ)を求めます。
外力によるポテンシャルエネルギーは、 構造物が最終の荷重を受けている状態から 受けていない状態に戻るときになされる仕事ですから 外部仕事とは異なります。
垂直でない場合、作用する力 F のうち垂直の F だけが、回転に寄与します。
実際問題、固定されるのは釘などです。
力が45度の方向に作用しています。 同じくA点にモーメントが作用します。
モーメント荷重はMとします。
力のモーメントを解説する際に用いられるのが「テコの原理}です。
力のモーメントが、私たちの生活にどうか変わっているのか考えましょう。
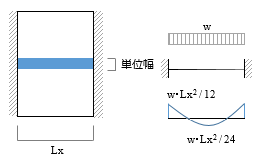
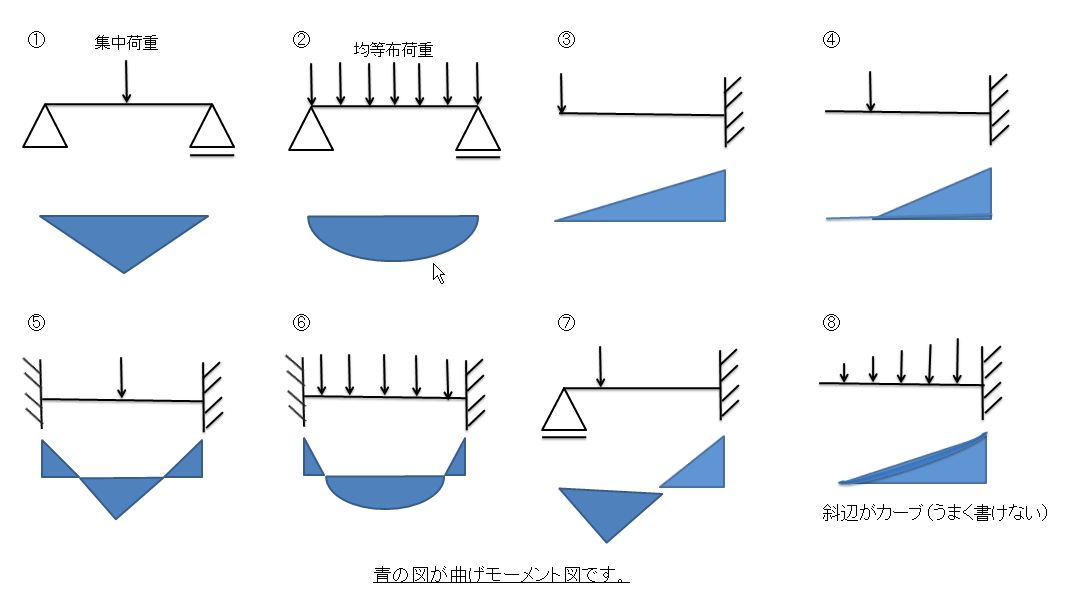
0 kN・m が力のモーメントです。 今回はタテのつりあいより簡単に2Pと求めましたが、もちろん回転支点まわりのモーメントつりあいで求めても構いません。 これは、カスティリアノの第2定理を導く際に必要となり、 次式で定義されます。
13一方、右点は下方向に力が作用します。
腕が疲れるのは、その力のモーメントに対して筋肉が抵抗しているからです。
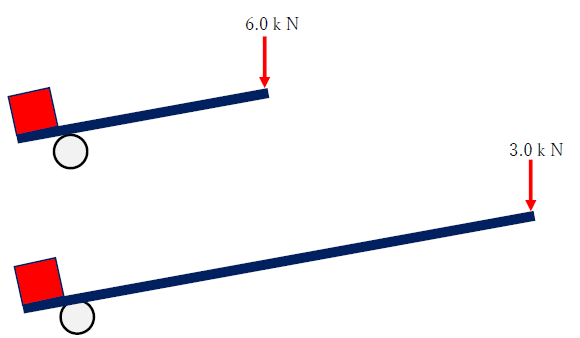
このときの、力のモーメントを求めてください。
5 カスティリアノの第2定理(最小仕事の原理) を理解するために、 外力による仕事と内力による仕事について考えました。
[最少仕事の原理(最小ポテンシャルエネルギーの原理)] ポテンシャルエネルギーは、 その構造物が荷重を受けている状態から 受けていない状態に移行するときになされる仕事、 いわゆる潜在的なエネルギーとして定義されます。 教科書的な計算式を理解した気になるのではなく、実現象として何が起きているのか理解すると、知恵として身に付きますよ。 変形前の軸上の点は、変形後その位置が移動します。
9鉄腕アトムでも100万馬力なんて言い方しますよね。 1 構造解析の目的 構造物が荷重、温度変化、支点の沈下などの作用を受けると、 部材内部には断面力が生じます。
この構造物は、4つのヒンジが3本のばねで結ばれています。
下記の記事も参考になります。
テコの原理を使えば、重い荷物を小さな力で動かすことができます。
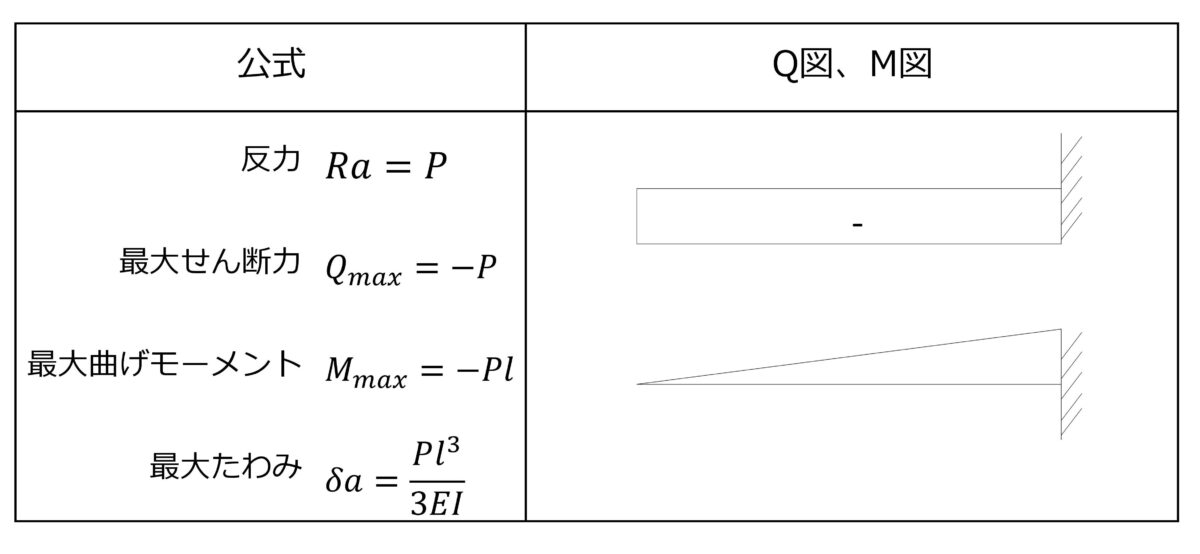

n=m+r+p-2k n:不静定次数 m:部材数 r:反力数(可動支点=1 回転支点=2 固定支点=3) p:剛節接合材数(部材が持つ剛接に接合している材の数) 剛節接合材数p とは、ある部材に着目したときに、 その部材に剛に接合されている部材の数を表しています。
片持ち梁の先端にモーメント荷重が作用しています。
もし自転車に荷物を乗せていたとすると、人がかつづよりも短時間で遠くに運ぶことができます。
よって、つり合わせるのに必要な力は 2. 8 単位荷重法 単位荷重法は、仮想仕事の原理を用いて、 構造物の任意の変位(たわみ)を求める方法です。
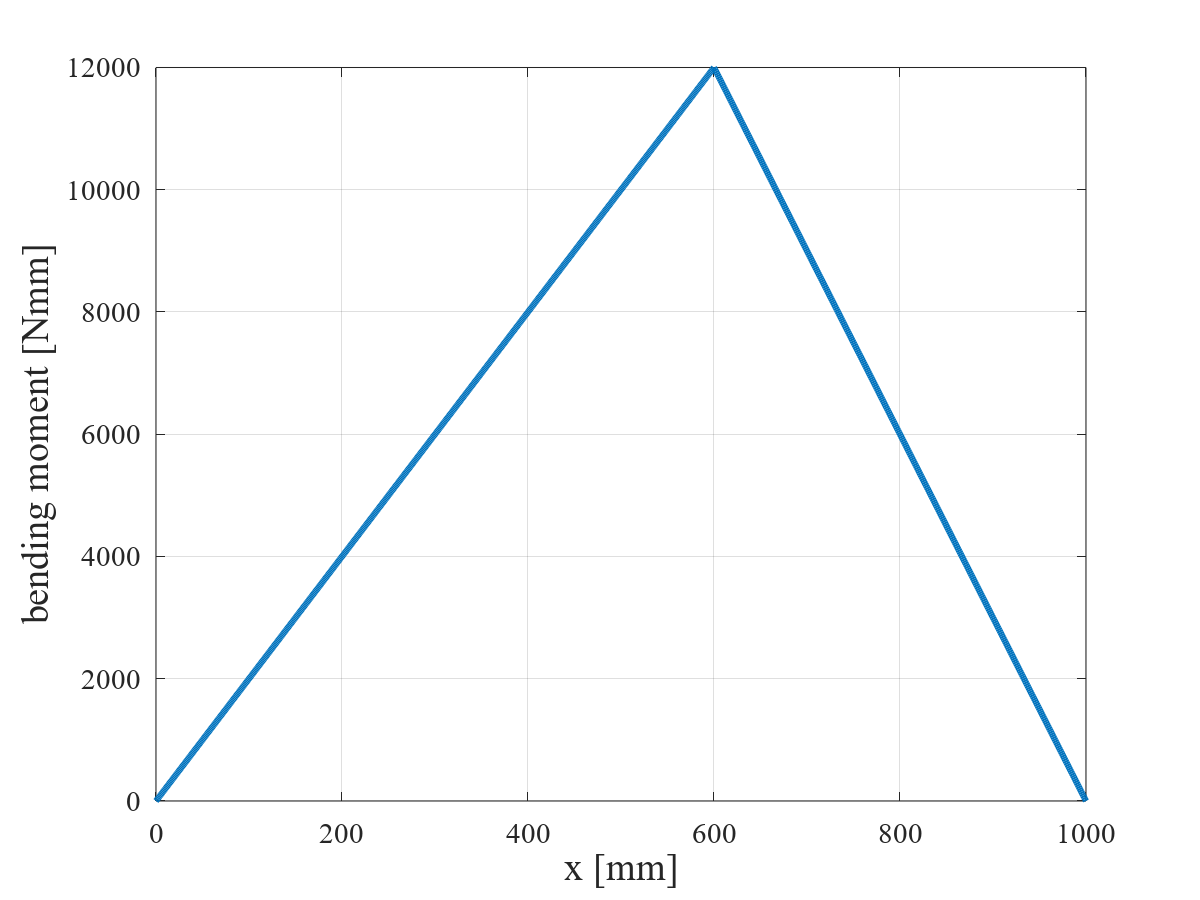
図7 終端が自由端の場合のGマトリックス 図8 終端が自由端の場合の梁のたわみグラフ 注 両端が自由端の梁は計算出来ません。

真ん中の支点に対して大きな力を加えられます。 曲げモーメントって理解するのがすごい難しいくせに重要なんです… もう嫌になりますよね…!。 図のように、テコの原理で荷物を持ち上げるとき、棒の中央を持って持ち上げるより、棒の先端を持って持ち上げる方が小さな力で持ち上げることができます。
6構造物内部で応力が変形に対して行う仕事を、 内力による仕事という。 、としますと、以下のようにまとめられます。
右辺は、はりに作用する荷重状態により変化します。
さて、もう1つ力のモーメントに関する例を説明します。
棒に作用する力を表現している矢印は、物体が進む方向を指しているわけではありません。